| Copyright | (c) Justus Sagemüller 2015 |
|---|---|
| License | GPL v3 |
| Maintainer | (@) jsag $ hvl.no |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | None |
| Language | Haskell2010 |
Data.Manifold.TreeCover
Description
Synopsis
- data Shade x where
- Shade :: (Semimanifold x, SimpleSpace (Needle x)) => {..} -> Shade x
- pattern (:±) :: () => (Semimanifold x, SimpleSpace (Needle x)) => Interior x -> [Needle x] -> Shade x
- data Shade' x = Shade' {
- _shade'Ctr :: !(Interior x)
- _shade'Narrowness :: !(Metric x)
- (|±|) :: forall x. WithField ℝ EuclidSpace x => x -> [Needle x] -> Shade' x
- class IsShade shade
- shadeCtr :: IsShade shade => Lens' (shade x) (Interior x)
- shadeExpanse :: Lens' (Shade x) (Metric' x)
- shadeNarrowness :: Lens' (Shade' x) (Metric x)
- fullShade :: (Semimanifold x, SimpleSpace (Needle x)) => Interior x -> Metric' x -> Shade x
- fullShade' :: WithField ℝ SimpleSpace x => Interior x -> Metric x -> Shade' x
- pointsShades :: (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade x]
- pointsShade's :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade' x]
- pointsCovers :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade x]
- pointsCover's :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade' x]
- coverAllAround :: forall x s. (Fractional' s, WithField s PseudoAffine x, SimpleSpace (Needle x)) => Interior x -> [Needle x] -> Shade x
- occlusion :: (IsShade shade, PseudoAffine x, SimpleSpace (Needle x), s ~ Scalar (Needle x), RealFloat' s) => shade x -> x -> s
- prettyShowsPrecShade' :: LtdErrorShow m => Int -> Shade' m -> ShowS
- prettyShowShade' :: LtdErrorShow x => Shade' x -> String
- factoriseShade :: (IsShade shade, PseudoAffine x, SimpleSpace (Needle x), PseudoAffine y, SimpleSpace (Needle y), Scalar (Needle x) ~ Scalar (Needle y)) => shade (x, y) -> (shade x, shade y)
- intersectShade's :: forall y. Refinable y => NonEmpty (Shade' y) -> Maybe (Shade' y)
- linIsoTransformShade :: (IsShade shade, SimpleSpace x, SimpleSpace y, Scalar x ~ Scalar y, Num' (Scalar x)) => (x +> y) -> shade x -> shade y
- embedShade :: (IsShade shade, Semimanifold x, Semimanifold y, Object (Affine s) (Interior x), Object (Affine s) (Interior y), SemiInner (Needle x), SimpleSpace (Needle y)) => Embedding (Affine s) (Interior x) (Interior y) -> shade x -> shade y
- projectShade :: (IsShade shade, Semimanifold x, Semimanifold y, Object (Affine s) (Interior x), Object (Affine s) (Interior y), SimpleSpace (Needle x), SemiInner (Needle y)) => Embedding (Affine s) (Interior x) (Interior y) -> shade y -> shade x
- class (WithField ℝ PseudoAffine y, SimpleSpace (Needle y)) => Refinable y
- subShade' :: Refinable y => Shade' y -> Shade' y -> Bool
- refineShade' :: Refinable y => Shade' y -> Shade' y -> Maybe (Shade' y)
- convolveShade' :: Refinable y => Shade' y -> Shade' (Needle y) -> Shade' y
- coerceShade :: (IsShade shade, Manifold x, Manifold y, LocallyCoercible x y, SimpleSpace (Needle y)) => shade x -> shade y
- mixShade's :: forall y. (WithField ℝ Manifold y, SimpleSpace (Needle y)) => NonEmpty (Shade' y) -> Maybe (Shade' y)
- type ShadeTree x = x `Shaded` ()
- fromLeafPoints :: forall x. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => [x] -> ShadeTree x
- fromLeafPoints_ :: forall x y. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => [(x, y)] -> x `Shaded` y
- onlyLeaves :: WithField ℝ PseudoAffine x => (x `Shaded` y) -> [(x, y)]
- onlyLeaves_ :: WithField ℝ PseudoAffine x => ShadeTree x -> [x]
- indexShadeTree :: forall x y. (x `Shaded` y) -> Int -> Either Int ([x `Shaded` y], (x, y))
- treeLeaf :: forall x y f. Functor f => Int -> (y -> f y) -> (x `Shaded` y) -> Either Int (f (x `Shaded` y))
- positionIndex :: forall x y. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => Maybe (Metric x) -> (x `Shaded` y) -> x -> Maybe (Int, ([x `Shaded` y], (x, y)))
- entireTree :: forall x y. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => (x `Shaded` y) -> LeafyTree x y
- onlyNodes :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => ShadeTree x -> Trees x
- trunkBranches :: (x `Shaded` y) -> NonEmpty (LeafIndex, x `Shaded` y)
- nLeaves :: (x `Shaded` y) -> Int
- treeDepth :: (x `Shaded` y) -> Int
- type SimpleTree = GenericTree Maybe []
- type Trees = GenericTree [] []
- type NonEmptyTree = GenericTree NonEmpty []
- newtype GenericTree c b x = GenericTree {
- treeBranches :: c (x, GenericTree b b x)
- 朳 :: c (x, GenericTree b b x) -> GenericTree c b x
- class HasFlatView f where
- type FlatView f x
- flatView :: f x -> FlatView f x
- superFlatView :: f x -> [[x]]
- shadesMerge :: forall x. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => ℝ -> [Shade x] -> [Shade x]
- allTwigs :: forall x y. WithField ℝ PseudoAffine x => (x `Shaded` y) -> [Twig x y]
- twigsWithEnvirons :: forall x y. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => (x `Shaded` y) -> [(Twig x y, TwigEnviron x y)]
- type Twig x y = (Int, x `Shaded` y)
- type TwigEnviron x y = [Twig x y]
- seekPotentialNeighbours :: forall x y. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => (x `Shaded` y) -> x `Shaded` (y, [Int])
- completeTopShading :: forall x y. (WithField ℝ PseudoAffine x, WithField ℝ PseudoAffine y, SimpleSpace (Needle x), SimpleSpace (Needle y)) => (x `Shaded` y) -> [Shade' (x, y)]
- flexTwigsShading :: forall x y f. (WithField ℝ Manifold x, WithField ℝ Manifold y, SimpleSpace (Needle x), SimpleSpace (Needle y), Applicative f) => (Shade' (x, y) -> f (x, (Shade' y, LocalLinear x y))) -> (x `Shaded` y) -> f (x `Shaded` y)
- traverseTrunkBranchChoices :: Applicative f => ((Int, x `Shaded` y) -> (x `Shaded` y) -> f (x `Shaded` z)) -> (x `Shaded` y) -> f (x `Shaded` z)
- data Shaded x y
- = PlainLeaves [(x, y)]
- | DisjointBranches !LeafCount (NonEmpty (x `Shaded` y))
- | OverlappingBranches !LeafCount !(Shade x) (NonEmpty (DBranch x y))
- fmapShaded :: (Semimanifold x, SimpleSpace (Needle x)) => (y -> υ) -> (x `Shaded` y) -> x `Shaded` υ
- constShaded :: y -> (x `Shaded` y₀) -> x `Shaded` y
- zipTreeWithList :: (x `Shaded` w) -> NonEmpty y -> x `Shaded` (w, y)
- stiAsIntervalMapping :: (x ~ ℝ, y ~ ℝ) => (x `Shaded` y) -> [(x, ((y, Diff y), LinearMap ℝ x y))]
- spanShading :: forall x y. (WithField ℝ Manifold x, WithField ℝ Manifold y, SimpleSpace (Needle x), SimpleSpace (Needle y)) => (Shade x -> Shade y) -> ShadeTree x -> x `Shaded` y
- type DBranch x y = DBranch' x (x `Shaded` y)
- data DBranch' x c = DBranch {
- boughDirection :: !(Needle' x)
- boughContents :: !(Hourglass c)
- data Hourglass s = Hourglass {}
- unsafeFmapTree :: (NonEmpty (x, y) -> NonEmpty (ξ, υ)) -> (Needle' x -> Needle' ξ) -> (Shade x -> Shade ξ) -> (x `Shaded` y) -> ξ `Shaded` υ
- type AffineManifold m = (Atlas m, Manifold m, AffineSpace m, Needle m ~ Diff m, HasTrie (ChartIndex m))
- euclideanMetric :: EuclidSpace x => proxy x -> Metric x
Shades
A Shade is a very crude description of a region within a manifold. It
can be interpreted as either an ellipsoid shape, or as the Gaussian peak
of a normal distribution (use http://hackage.haskell.org/package/manifold-random
for actually sampling from that distribution).
For a precise description of an arbitrarily-shaped connected subset of a manifold,
there is Region, whose implementation is vastly more complex.
Constructors
| Shade | |
Fields
| |
Instances
pattern (:±) :: () => (Semimanifold x, SimpleSpace (Needle x)) => Interior x -> [Needle x] -> Shade x infixl 6 Source #
Span a Shade from a center point and multiple deviation-vectors.
A “co-shade” can describe ellipsoid regions as well, but unlike
Shade it can be unlimited / infinitely wide in some directions.
It does OTOH need to have nonzero thickness, which Shade needs not.
Constructors
| Shade' | |
Fields
| |
Instances
(|±|) :: forall x. WithField ℝ EuclidSpace x => x -> [Needle x] -> Shade' x infixl 6 Source #
Similar to :±, but instead of expanding the shade, each vector restricts it.
Iff these form a orthogonal basis (in whatever sense applicable), then both
methods will be equivalent.
Note that |±| is only possible, as such, in an inner-product space; in
general you need reciprocal vectors (Needle') to define a Shade'.
Minimal complete definition
shadeCtr, occlusion, factoriseShade, coerceShade, orthoShades, linIsoTransformShade, projectShade, embedShade
Instances
Lenses
Construction
fullShade :: (Semimanifold x, SimpleSpace (Needle x)) => Interior x -> Metric' x -> Shade x Source #
fullShade' :: WithField ℝ SimpleSpace x => Interior x -> Metric x -> Shade' x Source #
pointsShades :: (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade x] Source #
Attempt to find a Shade that describes the distribution of given points.
At least in an affine space (and thus locally in any manifold), this can be used to
estimate the parameters of a normal distribution from which some points were
sampled. Note that some points will be “outside” of the shade,
as happens for a normal distribution with some statistical likelyhood.
(Use pointsCovers if you need to prevent that.)
For nonconnected manifolds it will be necessary to yield separate shades for each connected component. And for an empty input list, there is no shade! Hence the result type is a list.
pointsShade's :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade' x] Source #
pointsCovers :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade x] Source #
Like pointsShades, but ensure that all points are actually in
the shade, i.e. if [ is the result then
Shade x₀ ex]metric (recipMetric ex) (p-x₀) ≤ 1p in the list.
pointsCover's :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => [Interior x] -> [Shade' x] Source #
coverAllAround :: forall x s. (Fractional' s, WithField s PseudoAffine x, SimpleSpace (Needle x)) => Interior x -> [Needle x] -> Shade x Source #
Evaluation
occlusion :: (IsShade shade, PseudoAffine x, SimpleSpace (Needle x), s ~ Scalar (Needle x), RealFloat' s) => shade x -> x -> s Source #
Check the statistical likelihood-density of a point being within a shade. This is taken as a normal distribution.
prettyShowsPrecShade' :: LtdErrorShow m => Int -> Shade' m -> ShowS Source #
prettyShowShade' :: LtdErrorShow x => Shade' x -> String Source #
Misc
factoriseShade :: (IsShade shade, PseudoAffine x, SimpleSpace (Needle x), PseudoAffine y, SimpleSpace (Needle y), Scalar (Needle x) ~ Scalar (Needle y)) => shade (x, y) -> (shade x, shade y) Source #
linIsoTransformShade :: (IsShade shade, SimpleSpace x, SimpleSpace y, Scalar x ~ Scalar y, Num' (Scalar x)) => (x +> y) -> shade x -> shade y Source #
embedShade :: (IsShade shade, Semimanifold x, Semimanifold y, Object (Affine s) (Interior x), Object (Affine s) (Interior y), SemiInner (Needle x), SimpleSpace (Needle y)) => Embedding (Affine s) (Interior x) (Interior y) -> shade x -> shade y Source #
projectShade :: (IsShade shade, Semimanifold x, Semimanifold y, Object (Affine s) (Interior x), Object (Affine s) (Interior y), SimpleSpace (Needle x), SemiInner (Needle y)) => Embedding (Affine s) (Interior x) (Interior y) -> shade y -> shade x Source #
Squash a shade down into a lower dimensional space.
class (WithField ℝ PseudoAffine y, SimpleSpace (Needle y)) => Refinable y Source #
Class of manifolds which can use Shade' as a basic set type.
This is easily possible for vector spaces with the default implementations.
Instances
subShade' :: Refinable y => Shade' y -> Shade' y -> Bool Source #
a means subShade' b ≡ Truea is fully contained in b, i.e. from
minusLogOcclusion' a p < 1minusLogOcclusion' b p < 1.
refineShade' :: Refinable y => Shade' y -> Shade' y -> Maybe (Shade' y) Source #
Intersection between two shades.
coerceShade :: (IsShade shade, Manifold x, Manifold y, LocallyCoercible x y, SimpleSpace (Needle y)) => shade x -> shade y Source #
mixShade's :: forall y. (WithField ℝ Manifold y, SimpleSpace (Needle y)) => NonEmpty (Shade' y) -> Maybe (Shade' y) Source #
Weakened version of intersectShade's. What this function calculates is
rather the weighted mean of ellipsoid regions. If you interpret the
shades as uncertain physical measurements with normal distribution,
it gives the maximum-likelyhood result for multiple measurements of the
same quantity.
Shade trees
fromLeafPoints :: forall x. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => [x] -> ShadeTree x Source #
Build a quite nicely balanced tree from a cloud of points, on any real manifold.
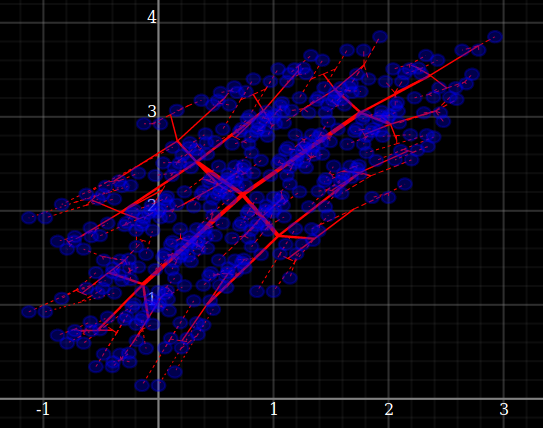
fromLeafPoints_ :: forall x y. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => [(x, y)] -> x `Shaded` y Source #
onlyLeaves :: WithField ℝ PseudoAffine x => (x `Shaded` y) -> [(x, y)] Source #
onlyLeaves_ :: WithField ℝ PseudoAffine x => ShadeTree x -> [x] Source #
Left (and, typically, also right) inverse of fromLeafNodes.
indexShadeTree :: forall x y. (x `Shaded` y) -> Int -> Either Int ([x `Shaded` y], (x, y)) Source #
The leaves of a shade tree are numbered. For a given index, this function attempts to find the leaf with that ID, within its immediate environment.
treeLeaf :: forall x y f. Functor f => Int -> (y -> f y) -> (x `Shaded` y) -> Either Int (f (x `Shaded` y)) Source #
Arguments
| :: (WithField ℝ Manifold x, SimpleSpace (Needle x)) | |
| => Maybe (Metric x) | For deciding (at the lowest level) what “close” means; this is optional for any tree of depth >1. |
| -> (x `Shaded` y) | The tree to index into |
| -> x | Position to look up |
| -> Maybe (Int, ([x `Shaded` y], (x, y))) | Index of the leaf near to the query point, the “path” of environment trees leading down to its position (in decreasing order of size), and actual position+info of the found node. |
“Inverse indexing” of a tree. This is roughly a nearest-neighbour search, but not guaranteed to give the correct result unless evaluated at the precise position of a tree leaf.
View helpers
entireTree :: forall x y. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => (x `Shaded` y) -> LeafyTree x y Source #
onlyNodes :: forall x. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => ShadeTree x -> Trees x Source #
Imitate the specialised ShadeTree structure with a simpler, generic tree.
Auxiliary types
type SimpleTree = GenericTree Maybe [] Source #
SimpleTreex ≅ Maybe (x,Treesx)
type NonEmptyTree = GenericTree NonEmpty [] Source #
NonEmptyTreex ≅ (x,Treesx)
newtype GenericTree c b x Source #
Constructors
| GenericTree | |
Fields
| |
Instances
朳 :: c (x, GenericTree b b x) -> GenericTree c b x Source #
U+6733 CJK UNIFIED IDEOGRAPH tree.
The main purpose of this is to give GenericTree a more concise Show instance.
Misc
class HasFlatView f where Source #
Arguments
| :: (WithField ℝ Manifold x, SimpleSpace (Needle x)) | |
| => ℝ | How near (inverse normalised distance, relative to shade expanse) two shades must be to be merged. If this is zero, any shades in the same connected region of a manifold are merged. |
| -> [Shade x] | A list of n shades. |
| -> [Shade x] | m ≤ n shades which cover at least the same area. |
Attempt to reduce the number of shades to fewer (ideally, a single one). In the simplest cases these should guaranteed cover the same area; for non-flat manifolds it only works in a heuristic sense.
twigsWithEnvirons :: forall x y. (WithField ℝ Manifold x, SimpleSpace (Needle x)) => (x `Shaded` y) -> [(Twig x y, TwigEnviron x y)] Source #
type TwigEnviron x y = [Twig x y] Source #
seekPotentialNeighbours :: forall x y. (WithField ℝ PseudoAffine x, SimpleSpace (Needle x)) => (x `Shaded` y) -> x `Shaded` (y, [Int]) Source #
completeTopShading :: forall x y. (WithField ℝ PseudoAffine x, WithField ℝ PseudoAffine y, SimpleSpace (Needle x), SimpleSpace (Needle y)) => (x `Shaded` y) -> [Shade' (x, y)] Source #
flexTwigsShading :: forall x y f. (WithField ℝ Manifold x, WithField ℝ Manifold y, SimpleSpace (Needle x), SimpleSpace (Needle y), Applicative f) => (Shade' (x, y) -> f (x, (Shade' y, LocalLinear x y))) -> (x `Shaded` y) -> f (x `Shaded` y) Source #
traverseTrunkBranchChoices :: Applicative f => ((Int, x `Shaded` y) -> (x `Shaded` y) -> f (x `Shaded` z)) -> (x `Shaded` y) -> f (x `Shaded` z) Source #
Constructors
| PlainLeaves [(x, y)] | |
| DisjointBranches !LeafCount (NonEmpty (x `Shaded` y)) | |
| OverlappingBranches !LeafCount !(Shade x) (NonEmpty (DBranch x y)) |
Instances
fmapShaded :: (Semimanifold x, SimpleSpace (Needle x)) => (y -> υ) -> (x `Shaded` y) -> x `Shaded` υ Source #
constShaded :: y -> (x `Shaded` y₀) -> x `Shaded` y Source #
stiAsIntervalMapping :: (x ~ ℝ, y ~ ℝ) => (x `Shaded` y) -> [(x, ((y, Diff y), LinearMap ℝ x y))] Source #
spanShading :: forall x y. (WithField ℝ Manifold x, WithField ℝ Manifold y, SimpleSpace (Needle x), SimpleSpace (Needle y)) => (Shade x -> Shade y) -> ShadeTree x -> x `Shaded` y Source #
Constructors
| DBranch | |
Fields
| |
Instances
Hourglass as the geometric shape (two opposing ~conical volumes, sharing only a single point in the middle); has nothing to do with time.
Instances
unsafeFmapTree :: (NonEmpty (x, y) -> NonEmpty (ξ, υ)) -> (Needle' x -> Needle' ξ) -> (Shade x -> Shade ξ) -> (x `Shaded` y) -> ξ `Shaded` υ Source #
External
type AffineManifold m = (Atlas m, Manifold m, AffineSpace m, Needle m ~ Diff m, HasTrie (ChartIndex m)) Source #
The AffineSpace class plus manifold constraints.
euclideanMetric :: EuclidSpace x => proxy x -> Metric x Source #
