Data.Stack

Stack data structure and associated operations

A stack is a basic data structure that can be logically thought as linear structure represented by a real physical stack or pile, a structure where insertion and deletion of items takes place at one end called top of the stack.

In other words, a Stack is an abstract data type that serves as a collection of elements, with two principal operations: stackPush, which adds an element to the collection, and stackPop, which removes the most recently added element that was not yet removed.

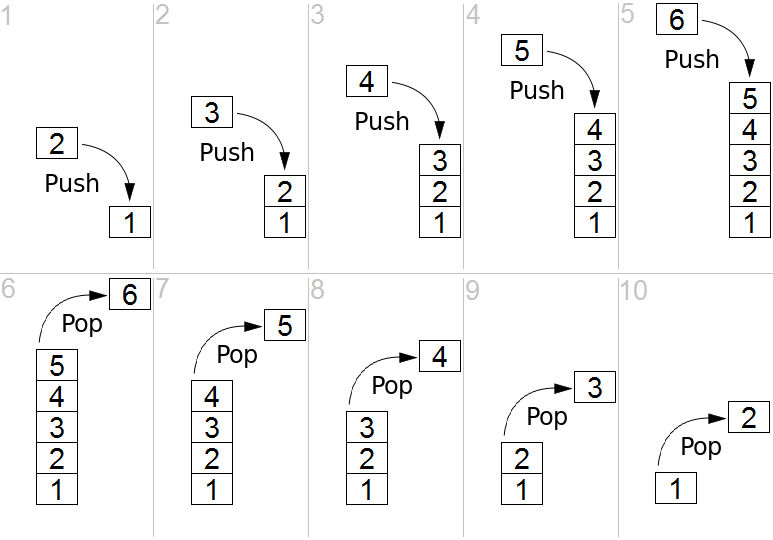
See also https://en.wikipedia.org/wiki/Stack_(abstract_data_type)

Documentation

data Stack a

Abstract Stack data type

Instances

Read a => Read (Stack a)

Defined in Data.Stack

Methods

readsPrec :: Int -> ReadS (Stack a)

readList :: ReadS [Stack a]

readPrec :: ReadPrec (Stack a)

readListPrec :: ReadPrec [Stack a]

Show a => Show (Stack a)

Defined in Data.Stack

Methods

showsPrec :: Int -> Stack a -> ShowS

show :: Stack a -> String

showList :: [Stack a] -> ShowS

Semigroup (Stack a)

Defined in Data.Stack

Methods

(<>) :: Stack a -> Stack a -> Stack a

sconcat :: NonEmpty (Stack a) -> Stack a

stimes :: Integral b => b -> Stack a -> Stack a

Monoid (Stack a)

Defined in Data.Stack

Methods

mempty :: Stack a

mappend :: Stack a -> Stack a -> Stack a

mconcat :: [Stack a] -> Stack a

NFData a => NFData (Stack a)

Defined in Data.Stack

Methods

rnf :: Stack a -> ()

stackNew :: Stack a

O(1). Create new empty Stack

stackPush :: Stack a -> a -> Stack a

O(1). Push item onto Stack

(∀x)(∀s)(stackPop (stackPush s x) == Just (s,x))

stackPeek :: Stack a -> Maybe a

O(1). Pop most recently added item without removing from the Stack

stackPeek stackNew == Nothing
(∀x)(∀s)(stackPeek (stackPush s x) == Just x)
(∀s)(stackPeek s == fmap snd (stackPop s))

stackPop :: Stack a -> Maybe (Stack a, a)

O(1). Pop most recently added item from Stack

stackPop stackNew == Nothing
(∀x)(∀s)(stackPop (stackPush s x) == Just (s,x))

stackIsEmpty :: Stack a -> Bool

O(1). Test if stack is empty

stackIsEmpty stackNew == True
(∀x)(∀s)(stackIsEmpty (stackPush s x) == True)
(∀s)((stackSize s == 0) ⇔ (stackIsEmpty s == True))

stackSize :: Stack a -> Natural

O(1). Compute number of elements contained in the Stack

stackSize stackNew == 0
(∀x)(∀s)((stackSize s == n) ⇒ (stackSize (stackPush s x) == n+1))