| Copyright | (C) 2017 Maksymilian Owsianny |
|---|---|
| License | BSD-style (see LICENSE) |
| Maintainer | Maksymilian.Owsianny@gmail.com |
| Safe Haskell | None |
| Language | Haskell2010 |
Geometry.SetOperations
Contents
Description
Set Operations of Polytopes. You can read about implementation details of this algorithm in a dedicated Blog Post.
Small example:
test :: SetOperation -> Double -> PolyT3D
test op t = fromVolume $ merge op boxA boxB
where
boxA = cube
boxB = toVolume $ Poly3 (papply tr <$> ps) is
Poly3 ps is = cubePoly3
tr = translation (V3 (sin (t*0.3) * 0.3) 0.2 0.3)
<> aboutX (t*20 @@ deg)
<> aboutY (t*3 @@ deg)Rendered:
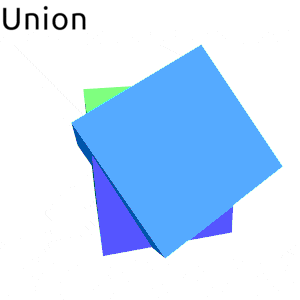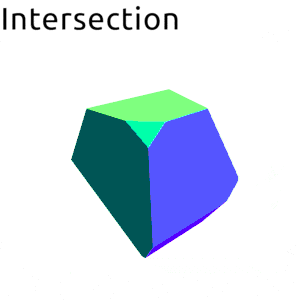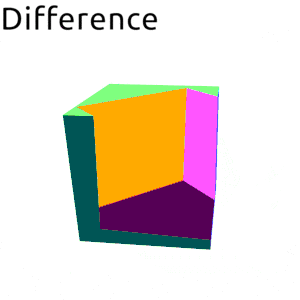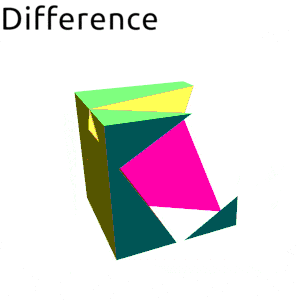
- data Volume b v n
- emptyVolume :: Volume b v n
- toVolume :: (FromPolytopeRep p b v n, Clip b v n, Functor v, Num n) => p v n -> Volume b v n
- fromVolume :: ToPolytopeRep p b v n => Volume b v n -> p v n
- data SetOperation
- merge :: Merge b v n => SetOperation -> Volume b v n -> Volume b v n -> Volume b v n
- merges :: Merge b v n => SetOperation -> [Volume b v n] -> Volume b v n
- union :: Merge b v n => Volume b v n -> Volume b v n -> Volume b v n
- unions :: Merge b v n => [Volume b v n] -> Volume b v n
- intersection :: Merge b v n => Volume b v n -> Volume b v n -> Volume b v n
- intersections :: Merge b v n => [Volume b v n] -> Volume b v n
- difference :: Merge b v n => Volume b v n -> Volume b v n -> Volume b v n
- differences :: Merge b v n => Volume b v n -> [Volume b v n] -> Volume b v n
- class FromPolytopeRep p b v n
- class ToPolytopeRep p b v n
- data Poly3 v n = Poly3 (Vector (Point v n)) [[Int]]
- newtype PolyT3 v n = PolyT3 [[Point v n]]
- cubePoly3 :: Poly3D
- cube :: Volume3D
- toVolume3D :: Poly3D -> Volume3D
- fromVolume3D :: Volume3D -> PolyT3D
Base Functionality
emptyVolume :: Volume b v n Source #
Empty volume.
toVolume :: (FromPolytopeRep p b v n, Clip b v n, Functor v, Num n) => p v n -> Volume b v n Source #
Convert an arbitrary polytope boundary representation into a Volume.
fromVolume :: ToPolytopeRep p b v n => Volume b v n -> p v n Source #
Recover a boundary representation of a Volume.
data SetOperation Source #
Four basic set operations:

Constructors
| Union | |
| Intersection | |
| Difference | |
| SymmetricDifference |
merge :: Merge b v n => SetOperation -> Volume b v n -> Volume b v n -> Volume b v n Source #
Merge two Volumes under a specified Set Operation.
merges :: Merge b v n => SetOperation -> [Volume b v n] -> Volume b v n Source #
Merges list of Volumes under a specified Set Operation. Empty list equals empty set.
Selected Merge Operations
union :: Merge b v n => Volume b v n -> Volume b v n -> Volume b v n Source #
Union of two volumes. Convenience synonym for `merge Union`
intersection :: Merge b v n => Volume b v n -> Volume b v n -> Volume b v n Source #
Intersection of two volumes.
intersections :: Merge b v n => [Volume b v n] -> Volume b v n Source #
Intersection of list of volumes.
difference :: Merge b v n => Volume b v n -> Volume b v n -> Volume b v n Source #
Difference between two volumes.
differences :: Merge b v n => Volume b v n -> [Volume b v n] -> Volume b v n Source #
Subtract list of volumes from a given volume.
Conversion from/to BReps
class FromPolytopeRep p b v n Source #
Convert from polytope to a list of Facets.
Minimal complete definition
class ToPolytopeRep p b v n Source #
Convert from list of Facets to a polytope boundary representation.
Minimal complete definition
Instances
| ToPolytopeRep PolyT3 (FB3 v n) v n Source # | |
Indexed 3-BRep as a list of convex polygons. Continent as a way to introduce new base shapes into the constructive geometry context.
Simple direct 3-BRep as a list of triangles. Useful as an output after performing specified set operations of the base shapes for rendering.
Instances
| ToPolytopeRep PolyT3 (FB3 v n) v n Source # | |
Primitives
Specializations/Synonyms
toVolume3D :: Poly3D -> Volume3D Source #
Convert a simple 3-BRep polyhedron to a Volume.
fromVolume3D :: Volume3D -> PolyT3D Source #
Reconstruct a triangulated 3-BRep from a Volume.