Kleene

Kleene algebra.

This package provides means to work with kleene algebra, at the moment specifically concentrating on regular expressions over Char.

Implements ideas from Regular-expression derivatives re-examined by Scott Owens, John Reppy and Aaron Turon https://doi.org/10.1017/S0956796808007090.

>>> :set -XOverloadedStrings
>>> import Algebra.Lattice
>>> import Algebra.PartialOrd
>>> import Data.Semigroup
>>> import Kleene.Internal.Pretty (putPretty)

Kleene.RE module provides RE type. Kleene.Classes module provides various classes to work with the type. All of that is re-exported from Kleene module.

First let's construct a regular expression value:

>>> let re = star "abc" <> "def" <> ("x" \/ "yz") :: RE Char
>>> putPretty re
^(abc)*def(x|yz)$

We can convert it to DFA (there are 8 states)

>>> let dfa = fromTM re
>>> putPretty dfa
0 -> \x -> if
    | x <= '`'  -> 8
    | x <= 'a'  -> 5
    | x <= 'c'  -> 8
    | x <= 'd'  -> 3
    | otherwise -> 8
1 -> \x -> if
    | x <= 'w'  -> 8
    | x <= 'x'  -> 6
    | x <= 'y'  -> 7
    | otherwise -> 8
2 -> ...
...

It's also possible to graphically visualise DFAs

λ> writeFile "example.dot' (toDot dfa)
%  dot -Tpng -oexample.png example.dot

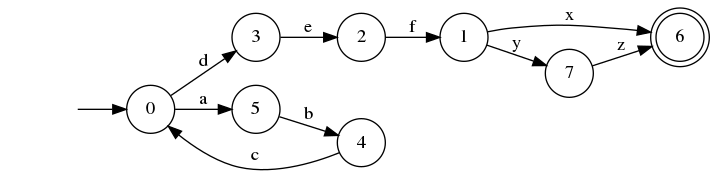
And we can convert back from DFA to RE:

>>> let re' = toKleene dfa :: RE Char
>>> putPretty re'
^(a(bca)*bcdefx|defx|(a(bca)*bcdefy|defy)z)$

As you see, we don't get what we started with. Yet, these regular expressions are equivalent;

>>> equivalent re re'
True

or using Equiv wrapper

>>> Equiv re == Equiv re'
True

(The paper doesn't outline decision procedure for the equivalence, though it's right there - seems to be fast enough at least for toy examples like here).

We can use regular expressions to generate word examples in the language:

>>> import Data.Foldable
>>> import qualified Test.QuickCheck as QC
>>> import Kleene.RE (generate)

>>> traverse_ print $ take 5 $ generate (curry QC.choose) 42 re
"abcabcabcabcabcabcdefyz"
"abcabcabcabcdefyz"
"abcabcabcabcabcabcabcabcabcdefx"
"abcabcdefx"
"abcabcabcabcabcabcdefyz"

In addition to the "normal" regular expressions, there are extended regular expressions. Regular expressions which we can complement, and therefore intersect:

>>> let ere = star "aa" /\ star "aaa" :: ERE Char
>>> putPretty ere
^~(~((aa)*)|~((aaa)*))$

We can convert ERE to RE via DFA:

>>> let re'' = toKleene (fromTM ere) :: RE Char
>>> putPretty re''
^(a(aaaaaa)*aaaaa)?$

Machine works own ways, we don't (always) get as pretty results as we'd like:

>>> equivalent re'' (star "aaaaaa")
True

Another feature of the library is an Applciative Functor,

>>> import Control.Applicative
>>> import qualified Kleene.Functor as F

>>> let f = (,) <$> many (F.char 'x') <* F.few F.anyChar <*> many (F.char 'z')
>>> putPretty f
^x*[^]*z*$

By relying on http://hackage.haskell.org/package/regex-applicative library, we can match and capture with regular expression.

>>> F.match f "xyyzzz"
Just ("x","zzz")

Where with RE we can only get True or False:

>>> match (F.toRE f) "xyyzzz"
True

Which in this case is not even interesting because:

>>> equivalent (F.toRE f) everything
True

Converting from RE to K is also possible, which may be handy:

>>> let g = (,) <$> F.few F.anyChar <*> F.fromRE re''
>>> putPretty g
^[^]*(a(aaaaaa)*aaaaa)?$

>>> F.match g (replicate 20 'a')
Just ("aa","aaaaaaaaaaaaaaaaaa")

We got longest divisible by 6 prefix of as. That's because fromRE uses many for star.

Regular expressions

data RE c

Regular expression

Constructors are exposed, but you should use smart constructors in this module to construct RE.

The Eq and Ord instances are structural. The Kleene etc constructors do "weak normalisation", so for values constructed using those operations Eq witnesses "weak equivalence". See equivalent for regular-expression equivalence.

Structure is exposed in Kleene.RE module but consider constructors as half-internal. There are soft-invariants, but violating them shouldn't break anything in the package. (e.g. transitionMap will eventually terminate, but may create more redundant states if starting regexp is not "weakly normalised").

Instances

ToLatin1 RE

Defined in Kleene.Internal.RE

Methods

toLatin1 :: RE Char -> RE Word8

(Ord c, Enum c, Bounded c) => Complement c (RE c)

Defined in Kleene.DFA

Methods

complement :: RE c -> RE c

(Ord c, Enum c, Bounded c) => TransitionMap c (RE c)

Defined in Kleene.Internal.RE

Methods

transitionMap :: RE c -> Map (RE c) (SF c (RE c))

(Ord c, Enum c, Bounded c) => Equivalent c (RE c)

Defined in Kleene.Internal.RE

Methods

equivalent :: RE c -> RE c -> Bool

(Ord c, Enum c, Bounded c) => Match c (RE c)

Defined in Kleene.Internal.RE

Methods

match :: RE c -> [c] -> Bool

match8 :: RE c -> ByteString -> Bool

(Ord c, Enum c, Bounded c) => Derivate c (RE c)

Defined in Kleene.Internal.RE

Methods

nullable :: RE c -> Bool

derivate :: c -> RE c -> RE c

(Ord c, Enum c, Bounded c) => FiniteKleene c (RE c)

Defined in Kleene.Internal.RE

Methods

everything :: RE c

charRange :: c -> c -> RE c

fromRSet :: RSet c -> RE c

dot :: RE c

anyChar :: RE c

notChar :: c -> RE c

(Ord c, Enum c, Bounded c) => CharKleene c (RE c)

Defined in Kleene.Internal.RE

Methods

char :: c -> RE c

string :: [c] -> RE c

Eq c => Eq (RE c)

Defined in Kleene.Internal.RE

Methods

(==) :: RE c -> RE c -> Bool

(/=) :: RE c -> RE c -> Bool

Ord c => Ord (RE c)

Defined in Kleene.Internal.RE

Methods

compare :: RE c -> RE c -> Ordering

(<) :: RE c -> RE c -> Bool

(<=) :: RE c -> RE c -> Bool

(>) :: RE c -> RE c -> Bool

(>=) :: RE c -> RE c -> Bool

max :: RE c -> RE c -> RE c

min :: RE c -> RE c -> RE c

Show c => Show (RE c)

Defined in Kleene.Internal.RE

Methods

showsPrec :: Int -> RE c -> ShowS

show :: RE c -> String

showList :: [RE c] -> ShowS

c ~ Char => IsString (RE c)

Defined in Kleene.Internal.RE

Methods

fromString :: String -> RE c

Eq c => Semigroup (RE c)

Defined in Kleene.Internal.RE

Methods

(<>) :: RE c -> RE c -> RE c

sconcat :: NonEmpty (RE c) -> RE c

stimes :: Integral b => b -> RE c -> RE c

Eq c => Monoid (RE c)

Defined in Kleene.Internal.RE

Methods

mempty :: RE c

mappend :: RE c -> RE c -> RE c

mconcat :: [RE c] -> RE c

(Ord c, Enum c, Bounded c, Arbitrary c) => Arbitrary (RE c)

Defined in Kleene.Internal.RE

Methods

arbitrary :: Gen (RE c)

shrink :: RE c -> [RE c]

CoArbitrary c => CoArbitrary (RE c)

Defined in Kleene.Internal.RE

Methods

coarbitrary :: RE c -> Gen b -> Gen b

(Ord c, Enum c, Bounded c) => Lattice (RE c)

WARNING: The /\ is inefficient, it actually computes the conjunction:

>>> putPretty $ asREChar $ "a" /\ "b"
^[]$

>>> putPretty $ asREChar $ "a" /\ star "a"
^a$

>>> putPretty $ asREChar $ star "aa" /\ star "aaa"
^(a(aaaaaa)*aaaaa)?$

Defined in Kleene.DFA

Methods

(\/) :: RE c -> RE c -> RE c

(/\) :: RE c -> RE c -> RE c

(Ord c, Enum c, Bounded c) => BoundedJoinSemiLattice (RE c)

Defined in Kleene.DFA

Methods

bottom :: RE c

(Ord c, Enum c, Bounded c) => BoundedMeetSemiLattice (RE c)

Defined in Kleene.DFA

Methods

top :: RE c

c ~ Char => Pretty (RE c)

Defined in Kleene.Internal.RE

Methods

pretty :: RE c -> String

prettyS :: RE c -> ShowS

(Ord c, Enum c, Bounded c) => Kleene (RE c)

Defined in Kleene.Internal.RE

Methods

empty :: RE c

eps :: RE c

appends :: [RE c] -> RE c

unions :: [RE c] -> RE c

star :: RE c -> RE c

data ERE c

Extended regular expression

It's both, Kleene and Boolean algebra. (If we add only intersections, it wouldn't be Boolean).

Note: we don't have special constructor for intersections. We use de Morgan formula \(a \land b = \neg (\neg a \lor \neg b)\).

>>> putPretty $ asEREChar $ "a" /\ "b"
^~(~a|~b)$

There is no generator, as intersections makes it hard.

Instances

ToLatin1 ERE

Defined in Kleene.ERE

Methods

toLatin1 :: ERE Char -> ERE Word8

Complement c (ERE c)

Defined in Kleene.ERE

Methods

complement :: ERE c -> ERE c

(Ord c, Enum c, Bounded c) => TransitionMap c (ERE c)

Defined in Kleene.ERE

Methods

transitionMap :: ERE c -> Map (ERE c) (SF c (ERE c))

(Ord c, Enum c, Bounded c) => Equivalent c (ERE c)

Defined in Kleene.ERE

Methods

equivalent :: ERE c -> ERE c -> Bool

(Ord c, Enum c) => Match c (ERE c)

Defined in Kleene.ERE

Methods

match :: ERE c -> [c] -> Bool

match8 :: ERE c -> ByteString -> Bool

(Ord c, Enum c) => Derivate c (ERE c)

Defined in Kleene.ERE

Methods

nullable :: ERE c -> Bool

derivate :: c -> ERE c -> ERE c

(Ord c, Enum c, Bounded c) => FiniteKleene c (ERE c)

Defined in Kleene.ERE

Methods

everything :: ERE c

charRange :: c -> c -> ERE c

fromRSet :: RSet c -> ERE c

dot :: ERE c

anyChar :: ERE c

notChar :: c -> ERE c

(Ord c, Enum c, Bounded c) => CharKleene c (ERE c)

Defined in Kleene.ERE

Methods

char :: c -> ERE c

string :: [c] -> ERE c

Eq c => Eq (ERE c)

Defined in Kleene.ERE

Methods

(==) :: ERE c -> ERE c -> Bool

(/=) :: ERE c -> ERE c -> Bool

Ord c => Ord (ERE c)

Defined in Kleene.ERE

Methods

compare :: ERE c -> ERE c -> Ordering

(<) :: ERE c -> ERE c -> Bool

(<=) :: ERE c -> ERE c -> Bool

(>) :: ERE c -> ERE c -> Bool

(>=) :: ERE c -> ERE c -> Bool

max :: ERE c -> ERE c -> ERE c

min :: ERE c -> ERE c -> ERE c

Show c => Show (ERE c)

Defined in Kleene.ERE

Methods

showsPrec :: Int -> ERE c -> ShowS

show :: ERE c -> String

showList :: [ERE c] -> ShowS

c ~ Char => IsString (ERE c)

Defined in Kleene.ERE

Methods

fromString :: String -> ERE c

Eq c => Semigroup (ERE c)

Defined in Kleene.ERE

Methods

(<>) :: ERE c -> ERE c -> ERE c

sconcat :: NonEmpty (ERE c) -> ERE c

stimes :: Integral b => b -> ERE c -> ERE c

Eq c => Monoid (ERE c)

Defined in Kleene.ERE

Methods

mempty :: ERE c

mappend :: ERE c -> ERE c -> ERE c

mconcat :: [ERE c] -> ERE c

(Ord c, Enum c, Bounded c, Arbitrary c) => Arbitrary (ERE c)

Defined in Kleene.ERE

Methods

arbitrary :: Gen (ERE c)

shrink :: ERE c -> [ERE c]

CoArbitrary c => CoArbitrary (ERE c)

Defined in Kleene.ERE

Methods

coarbitrary :: ERE c -> Gen b -> Gen b

(Ord c, Enum c) => Lattice (ERE c)

Defined in Kleene.ERE

Methods

(\/) :: ERE c -> ERE c -> ERE c

(/\) :: ERE c -> ERE c -> ERE c

(Ord c, Enum c) => BoundedJoinSemiLattice (ERE c)

Defined in Kleene.ERE

Methods

bottom :: ERE c

(Ord c, Enum c) => BoundedMeetSemiLattice (ERE c)

Defined in Kleene.ERE

Methods

top :: ERE c

c ~ Char => Pretty (ERE c)

Defined in Kleene.ERE

Methods

pretty :: ERE c -> String

prettyS :: ERE c -> ShowS

(Ord c, Enum c, Bounded c) => Kleene (ERE c)

Defined in Kleene.ERE

Methods

empty :: ERE c

eps :: ERE c

appends :: [ERE c] -> ERE c

unions :: [ERE c] -> ERE c

star :: ERE c -> ERE c

Equivalence (and partial order)

newtype Equiv r c

Regular-expressions for which == is equivalent.

>>> let re1 = star "a" <> "a" :: RE Char
>>> let re2 = "a" <> star "a" :: RE Char

>>> re1 == re2
False

>>> Equiv re1 == Equiv re2
True

Equiv is also a PartialOrd (but not Ord!)

>>> Equiv "a" `leq` Equiv (star "a" :: RE Char)
True

Not all regular expessions are comparable:

>>> let reA = Equiv "a" :: Equiv RE Char
>>> let reB = Equiv "b" :: Equiv RE Char
>>> (leq reA reB, leq reB reA)
(False,False)

Constructors

Equiv (r c)

Instances

Complement c (r c) => Complement c (Equiv r c)

Defined in Kleene.Equiv

Methods

complement :: Equiv r c -> Equiv r c

Equivalent c (r c) => Equivalent c (Equiv r c)

Defined in Kleene.Equiv

Methods

equivalent :: Equiv r c -> Equiv r c -> Bool

Match c (r c) => Match c (Equiv r c)

Defined in Kleene.Equiv

Methods

match :: Equiv r c -> [c] -> Bool

match8 :: Equiv r c -> ByteString -> Bool

Derivate c (r c) => Derivate c (Equiv r c)

Defined in Kleene.Equiv

Methods

nullable :: Equiv r c -> Bool

derivate :: c -> Equiv r c -> Equiv r c

CharKleene c (r c) => CharKleene c (Equiv r c)

Defined in Kleene.Equiv

Methods

char :: c -> Equiv r c

string :: [c] -> Equiv r c

Equivalent c (r c) => Eq (Equiv r c)

Defined in Kleene.Equiv

Methods

(==) :: Equiv r c -> Equiv r c -> Bool

(/=) :: Equiv r c -> Equiv r c -> Bool

Show (r c) => Show (Equiv r c)

Defined in Kleene.Equiv

Methods

showsPrec :: Int -> Equiv r c -> ShowS

show :: Equiv r c -> String

showList :: [Equiv r c] -> ShowS

Semigroup (r c) => Semigroup (Equiv r c)

Defined in Kleene.Equiv

Methods

(<>) :: Equiv r c -> Equiv r c -> Equiv r c

sconcat :: NonEmpty (Equiv r c) -> Equiv r c

stimes :: Integral b => b -> Equiv r c -> Equiv r c

Monoid (r c) => Monoid (Equiv r c)

Defined in Kleene.Equiv

Methods

mempty :: Equiv r c

mappend :: Equiv r c -> Equiv r c -> Equiv r c

mconcat :: [Equiv r c] -> Equiv r c

Lattice (r c) => Lattice (Equiv r c)

Defined in Kleene.Equiv

Methods

(\/) :: Equiv r c -> Equiv r c -> Equiv r c

(/\) :: Equiv r c -> Equiv r c -> Equiv r c

BoundedJoinSemiLattice (r c) => BoundedJoinSemiLattice (Equiv r c)

Defined in Kleene.Equiv

Methods

bottom :: Equiv r c

BoundedMeetSemiLattice (r c) => BoundedMeetSemiLattice (Equiv r c)

Defined in Kleene.Equiv

Methods

top :: Equiv r c

(Lattice (r c), Equivalent c (r c)) => PartialOrd (Equiv r c)

\(a \preceq b := a \lor b = b \)

Defined in Kleene.Equiv

Methods

leq :: Equiv r c -> Equiv r c -> Bool

comparable :: Equiv r c -> Equiv r c -> Bool

Pretty (r c) => Pretty (Equiv r c)

Defined in Kleene.Equiv

Methods

pretty :: Equiv r c -> String

prettyS :: Equiv r c -> ShowS

Kleene (r c) => Kleene (Equiv r c)

Defined in Kleene.Equiv

Methods

empty :: Equiv r c

eps :: Equiv r c

appends :: [Equiv r c] -> Equiv r c

unions :: [Equiv r c] -> Equiv r c

star :: Equiv r c -> Equiv r c

Deterministic finite automaton

data DFA c

Deterministic finite automaton.

A deterministic finite automaton (DFA) over an alphabet \(\Sigma\) (type variable c) is 4-tuple \(Q\), \(q_0\) , \(F\), \(\delta\), where

• \(Q\) is a finite set of states (subset of s),
• \(q_0 \in Q\) is the distinguised start state (dfaInitial),
• \(F \subset Q\) is a set of final (or accepting) states (dfaAcceptable), and
• \(\delta : Q \times \Sigma \to Q\) is a function called the state transition function (dfaTransition).

Constructors

DFA

Fields

• dfaTransition :: !(IntMap (SF c Int))

  transition function

• dfaInitial :: !Int

  initial state

• dfaAcceptable :: !IntSet

  accept states

• dfaBlackholes :: !IntSet

  states we cannot escape

Instances

Complement c (DFA c)

Complement DFA.

Complement of DFA is way easier than of RE: complement accept states.

>>> let dfa = complement $ fromRE $ RE.star "abc"
>>> putPretty dfa
0 -> \x -> if
    | x <= '`'  -> 3
    | x <= 'a'  -> 2
    | otherwise -> 3
1+ -> \x -> if
    | x <= 'b'  -> 3
    | x <= 'c'  -> 0
    | otherwise -> 3
2+ -> \x -> if
    | x <= 'a'  -> 3
    | x <= 'b'  -> 1
    | otherwise -> 3
3+ -> \_ -> 3 -- black hole

>>> map (match dfa) ["", "abc", "abcabc", "aa","abca", 'a' : 'a' : undefined]
[False,False,False,True,True,True]

Defined in Kleene.DFA

Methods

complement :: DFA c -> DFA c

Ord c => Match c (DFA c)

Run DFA on the input.

Because we have analysed a language, in some cases we can determine a result without traversing all of the input. That's not the cases with RE match.

>>> let dfa = fromRE $ RE.star "abc"
>>> map (match dfa) ["", "abc", "abcabc", "aa", 'a' : 'a' : undefined]
[True,True,True,False,False]

Holds:

match (fromRE re) xs == match re xs

all (match (fromRE r)) $ take 10 $ RE.generate (curry QC.choose) 42 (r :: RE.RE Char)

Defined in Kleene.DFA

Methods

match :: DFA c -> [c] -> Bool

match8 :: DFA c -> ByteString -> Bool

Ord c => Derivate c (DFA c)

Defined in Kleene.DFA

Methods

nullable :: DFA c -> Bool

derivate :: c -> DFA c -> DFA c

Show c => Show (DFA c)

Defined in Kleene.DFA

Methods

showsPrec :: Int -> DFA c -> ShowS

show :: DFA c -> String

showList :: [DFA c] -> ShowS

Show c => Pretty (DFA c)

Defined in Kleene.DFA

Methods

pretty :: DFA c -> String

prettyS :: DFA c -> ShowS

fromTM :: forall k c. (Ord k, Ord c, TransitionMap c k) => k -> DFA c

Create from TransitionMap.

See fromRE for a specific example.

fromTMEquiv :: forall k c. (Ord k, Ord c, TransitionMap c k, Equivalent c k) => k -> DFA c

Create from TransitonMap minimising states with Equivalent.

See fromERE for an example.

toKleene :: forall k c. (Ord c, Enum c, Bounded c, FiniteKleene c k) => DFA c -> k

Convert to any Kleene.

See toRE for a specific example.

toDot :: DFA Char -> String

Get Graphviz dot-code of DFA.

>>> let dfa = fromRE $ RE.star "abc"
>>> putStr $ toDot dfa
digraph dfa {
rankdir=LR;
// states
"0" [shape=doublecircle];
"1" [shape=circle];
"2" [shape=circle];
// initial state
"" [shape=none];
"" -> "0";
// transitions
"0" -> "2"[label="a"]
"1" -> "0"[label="c"]
"2" -> "1"[label="b"]
}

Classes

Most operations are defined in following type-classes.

See Kleene.RE module for a specific version with examples.

class Kleene k where

Kleene algebra.

If k is Monoid it's expected that appends = mappend; if k is Lattice it's expected that unions = joins.

Wikipedia: Kleene Algebra.

Methods

empty :: k

Empty regex. Doesn't accept anything.

eps :: k

Empty string. Note: different than empty.

appends :: [k] -> k

Concatenation.

unions :: [k] -> k

Union.

star :: k -> k

Kleene star.

Instances

(Ord c, Enum c, Bounded c) => Kleene (RE c)

Defined in Kleene.Internal.RE

Methods

empty :: RE c

eps :: RE c

appends :: [RE c] -> RE c

unions :: [RE c] -> RE c

star :: RE c -> RE c

(Ord c, Enum c, Bounded c) => Kleene (ERE c)

Defined in Kleene.ERE

Methods

empty :: ERE c

eps :: ERE c

appends :: [ERE c] -> ERE c

unions :: [ERE c] -> ERE c

star :: ERE c -> ERE c

Kleene (M c)

Defined in Kleene.Monad

Methods

empty :: M c

eps :: M c

appends :: [M c] -> M c

unions :: [M c] -> M c

star :: M c -> M c

Kleene (r c) => Kleene (Equiv r c)

Defined in Kleene.Equiv

Methods

empty :: Equiv r c

eps :: Equiv r c

appends :: [Equiv r c] -> Equiv r c

unions :: [Equiv r c] -> Equiv r c

star :: Equiv r c -> Equiv r c

class Kleene k => CharKleene c k | k -> c where

Minimal complete definition

char

Methods

char :: c -> k

Single character

string :: [c] -> k

Instances

(Ord c, Enum c, Bounded c) => CharKleene c (RE c)

Defined in Kleene.Internal.RE

Methods

char :: c -> RE c

string :: [c] -> RE c

(Ord c, Enum c, Bounded c) => CharKleene c (ERE c)

Defined in Kleene.ERE

Methods

char :: c -> ERE c

string :: [c] -> ERE c

CharKleene c (M c)

Defined in Kleene.Monad

Methods

char :: c -> M c

string :: [c] -> M c

CharKleene c (r c) => CharKleene c (Equiv r c)

Defined in Kleene.Equiv

Methods

char :: c -> Equiv r c

string :: [c] -> Equiv r c

class CharKleene c k => FiniteKleene c k | k -> c where

Minimal complete definition

charRange, fromRSet, anyChar

Methods

everything :: k

Everything. \(\Sigma^\star\).

charRange :: c -> c -> k

charRange a z = ^[a-z]$.

fromRSet :: RSet c -> k

Generalisation of charRange.

dot :: c ~ Char => k

. Every character except new line \n.

anyChar :: k

Any character. Note: different than dot!

notChar :: c -> k

notChar :: (Ord c, Enum c, Bounded c) => c -> k

Instances

(Ord c, Enum c, Bounded c) => FiniteKleene c (RE c)

Defined in Kleene.Internal.RE

Methods

everything :: RE c

charRange :: c -> c -> RE c

fromRSet :: RSet c -> RE c

dot :: RE c

anyChar :: RE c

notChar :: c -> RE c

(Ord c, Enum c, Bounded c) => FiniteKleene c (ERE c)

Defined in Kleene.ERE

Methods

everything :: ERE c

charRange :: c -> c -> ERE c

fromRSet :: RSet c -> ERE c

dot :: ERE c

anyChar :: ERE c

notChar :: c -> ERE c

class Derivate c k | k -> c where

Methods

nullable :: k -> Bool

Does language contain an empty string?

derivate :: c -> k -> k

Derivative of a language.

Instances

(Ord c, Enum c, Bounded c) => Derivate c (RE c)

Defined in Kleene.Internal.RE

Methods

nullable :: RE c -> Bool

derivate :: c -> RE c -> RE c

(Ord c, Enum c) => Derivate c (ERE c)

Defined in Kleene.ERE

Methods

nullable :: ERE c -> Bool

derivate :: c -> ERE c -> ERE c

Ord c => Derivate c (DFA c)

Defined in Kleene.DFA

Methods

nullable :: DFA c -> Bool

derivate :: c -> DFA c -> DFA c

(Eq c, Enum c, Bounded c) => Derivate c (M c)

Defined in Kleene.Monad

Methods

nullable :: M c -> Bool

derivate :: c -> M c -> M c

Derivate c (r c) => Derivate c (Equiv r c)

Defined in Kleene.Equiv

Methods

nullable :: Equiv r c -> Bool

derivate :: c -> Equiv r c -> Equiv r c

class Match c k | k -> c where

An f can be used to match on the input.

Minimal complete definition

match

Methods

match :: k -> [c] -> Bool

match8 :: c ~ Word8 => k -> ByteString -> Bool

Instances

(Ord c, Enum c, Bounded c) => Match c (RE c)

Defined in Kleene.Internal.RE

Methods

match :: RE c -> [c] -> Bool

match8 :: RE c -> ByteString -> Bool

(Ord c, Enum c) => Match c (ERE c)

Defined in Kleene.ERE

Methods

match :: ERE c -> [c] -> Bool

match8 :: ERE c -> ByteString -> Bool

Ord c => Match c (DFA c)

Run DFA on the input.

Because we have analysed a language, in some cases we can determine a result without traversing all of the input. That's not the cases with RE match.

>>> let dfa = fromRE $ RE.star "abc"
>>> map (match dfa) ["", "abc", "abcabc", "aa", 'a' : 'a' : undefined]
[True,True,True,False,False]

Holds:

match (fromRE re) xs == match re xs

all (match (fromRE r)) $ take 10 $ RE.generate (curry QC.choose) 42 (r :: RE.RE Char)

Defined in Kleene.DFA

Methods

match :: DFA c -> [c] -> Bool

match8 :: DFA c -> ByteString -> Bool

(Eq c, Enum c, Bounded c) => Match c (M c)

Defined in Kleene.Monad

Methods

match :: M c -> [c] -> Bool

match8 :: M c -> ByteString -> Bool

Match c (r c) => Match c (Equiv r c)

Defined in Kleene.Equiv

Methods

match :: Equiv r c -> [c] -> Bool

match8 :: Equiv r c -> ByteString -> Bool

class Derivate c k => TransitionMap c k | k -> c where

Transition map.

Methods

transitionMap :: k -> Map k (SF c k)

Instances

(Ord c, Enum c, Bounded c) => TransitionMap c (RE c)

Defined in Kleene.Internal.RE

Methods

transitionMap :: RE c -> Map (RE c) (SF c (RE c))

(Ord c, Enum c, Bounded c) => TransitionMap c (ERE c)

Defined in Kleene.ERE

Methods

transitionMap :: ERE c -> Map (ERE c) (SF c (ERE c))

class Complement c k | k -> c where

Complement of the language.

Law:

match (complement f) xs = not (match f) xs

Methods

complement :: k -> k

Instances

Complement c (ERE c)

Defined in Kleene.ERE

Methods

complement :: ERE c -> ERE c

(Ord c, Enum c, Bounded c) => Complement c (RE c)

Defined in Kleene.DFA

Methods

complement :: RE c -> RE c

Complement c (DFA c)

Complement DFA.

Complement of DFA is way easier than of RE: complement accept states.

>>> let dfa = complement $ fromRE $ RE.star "abc"
>>> putPretty dfa
0 -> \x -> if
    | x <= '`'  -> 3
    | x <= 'a'  -> 2
    | otherwise -> 3
1+ -> \x -> if
    | x <= 'b'  -> 3
    | x <= 'c'  -> 0
    | otherwise -> 3
2+ -> \x -> if
    | x <= 'a'  -> 3
    | x <= 'b'  -> 1
    | otherwise -> 3
3+ -> \_ -> 3 -- black hole

>>> map (match dfa) ["", "abc", "abcabc", "aa","abca", 'a' : 'a' : undefined]
[False,False,False,True,True,True]

Defined in Kleene.DFA

Methods

complement :: DFA c -> DFA c

Complement c (r c) => Complement c (Equiv r c)

Defined in Kleene.Equiv

Methods

complement :: Equiv r c -> Equiv r c

class ToLatin1 k where

Methods

toLatin1 :: k Char -> k Word8

Instances

ToLatin1 RSet

Defined in Kleene.Classes

Methods

toLatin1 :: RSet Char -> RSet Word8

ToLatin1 RE

Defined in Kleene.Internal.RE

Methods

toLatin1 :: RE Char -> RE Word8

ToLatin1 ERE

Defined in Kleene.ERE

Methods

toLatin1 :: ERE Char -> ERE Word8

Functor

Only the type is exported so it can be referred to.

See Kleene.Functor for operations.

data K c a

Applicative Functor regular expression.

Instances

Functor (K c)

Defined in Kleene.Internal.Functor

Methods

fmap :: (a -> b) -> K c a -> K c b

(<$) :: a -> K c b -> K c a

Applicative (K c)

Defined in Kleene.Internal.Functor

Methods

pure :: a -> K c a

(<*>) :: K c (a -> b) -> K c a -> K c b

liftA2 :: (a -> b -> c0) -> K c a -> K c b -> K c c0

(*>) :: K c a -> K c b -> K c b

(<*) :: K c a -> K c b -> K c a

Alternative (K c)

Defined in Kleene.Internal.Functor

Methods

empty :: K c a

(<|>) :: K c a -> K c a -> K c a

some :: K c a -> K c [a]

many :: K c a -> K c [a]

Alt (K c)

Defined in Kleene.Internal.Functor

Methods

(<!>) :: K c a -> K c a -> K c a

some :: Applicative (K c) => K c a -> K c [a]

many :: Applicative (K c) => K c a -> K c [a]

Apply (K c)

Defined in Kleene.Internal.Functor

Methods

(<.>) :: K c (a -> b) -> K c a -> K c b

(.>) :: K c a -> K c b -> K c b

(<.) :: K c a -> K c b -> K c a

liftF2 :: (a -> b -> c0) -> K c a -> K c b -> K c c0

(c ~ Char, IsString a) => IsString (K c a)

Defined in Kleene.Internal.Functor

Methods

fromString :: String -> K c a

c ~ Char => Pretty (K c a)

Convert to non-matching JavaScript string which can be used as an argument to new RegExp

>>> putPretty ("foobar" :: K Char String)
^foobar$

>>> putPretty $ many ("foobar" :: K Char String)
^(foobar)*$

Defined in Kleene.Internal.Functor

Methods

pretty :: K c a -> String

prettyS :: K c a -> ShowS