Data.Function.Differentiable

Everywhere differentiable functions

data Differentiable s d c

The category of differentiable functions between manifolds over scalar s.

As you might guess, these offer automatic differentiation of sorts (basically, simple forward AD), but that's in itself is not really the killer feature here. More interestingly, we actually have the (à la Curry-Howard) proof built in: the function f has at x₀ derivative f'ₓ₀, if, for¹ ε>0, there exists δ such that |f x − (f x₀ + x⋅f'ₓ₀)| < ε for all |x − x₀| < δ.

Observe that, though this looks quite similar to the standard definition of differentiability, it is not equivalent thereto – in fact it does not prove any analytic properties at all. To make it equivalent, we need a lower bound on δ: simply δ gives us continuity, and for continuous differentiability, δ must grow at least like √ε for small ε. Neither of these conditions are enforced by the type system, but we do require them for any allowed values because these proofs are obviously tremendously useful – for instance, you can have a root-finding algorithm and actually be sure you get all solutions correctly, not just some that are (hopefully) the closest to some reference point you'd need to laborously define!

Unfortunately however, this also prevents doing any serious algebra with the category, because even something as simple as division necessary introduces singularities where the derivatives must diverge. Not to speak of many e.g. trigonometric functions that are undefined on whole regions. The PWDiffable and RWDiffable categories have explicit handling for those issues built in; you may simply use these categories even when you know the result will be smooth in your relevant domain (or must be, for e.g. physics reasons).

¹(The implementation does not deal with ε and δ as difference-bounding reals, but rather as metric tensors which define a boundary by prohibiting the overlap from exceeding one. This makes the category actually work on general manifolds.)

Instances

type UnitObject (Differentiable s) = ZeroDim s

type PointObject (Differentiable s) x = ()

type Object (Differentiable s) o = LocallyScalable s o

type PairObjects (Differentiable s) a b = ()

type AgentVal (Differentiable s) a v = GenericAgent (Differentiable s) a v

Region-wise defined diff'able functions

data RWDiffable s d c

Category of functions that, where defined, have an open region in which they are continuously differentiable. Hence RegionWiseDiff'able. Basically these are the partial version of PWDiffable.

Though the possibility of undefined regions is of course not too nice (we don't need Java to demonstrate this with its everywhere-looming null values...), this category will propably be the “workhorse” for most serious calculus applications, because it contains all the usual trig etc. functions and of course everything algebraic you can do in the reals.

The easiest way to define ordinary functions in this category is hence with its AgentValues, which have instances of the standard classes Num through Floating. For instance, the following defines the binary entropy as a differentiable function on the interval ]0,1[: (it will actually know where it's defined and where not. And I don't mean you need to exhaustively isNaN-check all results...)

hb :: RWDiffable ℝ ℝ ℝ
hb = alg (\p -> - p * logBase 2 p - (1-p) * logBase 2 (1-p) )

Instances

type UnitObject (RWDiffable s) = ZeroDim s

type PointObject (RWDiffable s) x = ()

type Object (RWDiffable s) o = (LocallyScalable s o, SimpleSpace (Needle o))

type PairObjects (RWDiffable s) a b = ()

type AgentVal (RWDiffable s) d c

Operators for piecewise definition

Because the agents of RWDiffable aren't really values in Hask, you can't use the standard comparison operators on them, nor the built-in syntax of guards or if-statements.

However, because this category allows functions to be undefined in some region, such decisions can be faked quite well: ?-> restricts a function to some region, by simply marking it undefined outside, and ?|: replaces these regions with values from another function.

Example: define a function that is compactly supported on the interval ]-1,1[, i.e. exactly zero everywhere outside.

Graphics.Dynamic.Plot.R2> plotWindow [fnPlot (\x -> -1 ?< x ?< 1 ?-> cos (x*pi/2)^2 ?|: 0)]

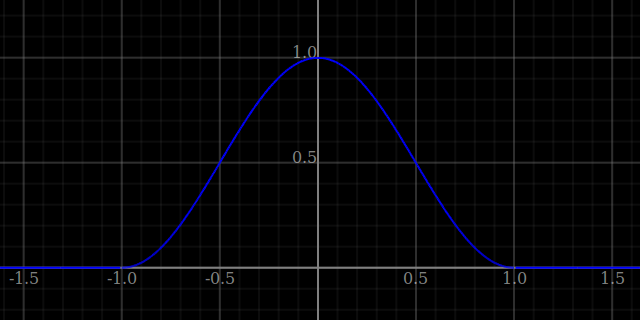
Note that it may not be necessary to restrict explicitly: for instance if a square root appears somewhere in an expression, then the expression is automatically restricted so that the root has a positive argument!

Graphics.Dynamic.Plot.R2> plotWindow [fnPlot (\x -> sqrt x ?|: -sqrt (-x))]

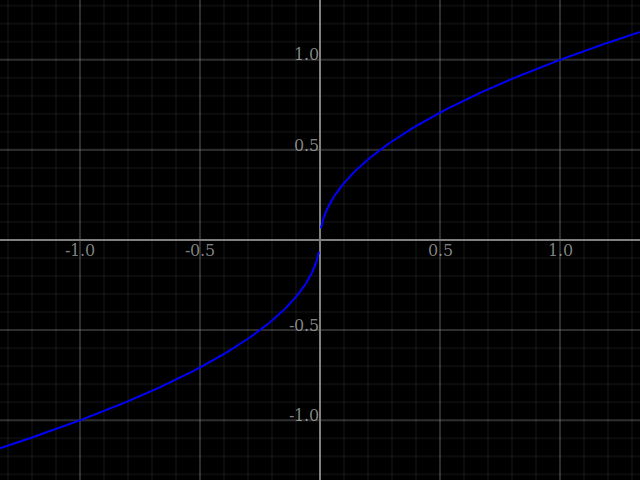
(?->) :: (RealDimension n, LocallyScalable n a, LocallyScalable n b, LocallyScalable n c, SimpleSpace (Needle b), SimpleSpace (Needle c)) => RWDfblFuncValue n c a -> RWDfblFuncValue n c b -> RWDfblFuncValue n c b infixr 4

Require the LHS to be defined before considering the RHS as result. This works analogously to the standard Applicative method

  (*>) :: Maybe a -> Maybe b -> Maybe b
  Just _ *> a = a
  _      *> a = Nothing
  

(?>) :: (RealDimension n, LocallyScalable n a, SimpleSpace (Needle a)) => RWDfblFuncValue n a n -> RWDfblFuncValue n a n -> RWDfblFuncValue n a n infixl 5

Return the RHS, if it is less than the LHS. (Really the purpose is just to compare the values, but returning one of them allows chaining of comparison operators like in Python.) Note that less-than comparison is equivalent to less-or-equal comparison, because there is no such thing as equality.

(?<) :: (RealDimension n, LocallyScalable n a, SimpleSpace (Needle a)) => RWDfblFuncValue n a n -> RWDfblFuncValue n a n -> RWDfblFuncValue n a n infixl 5

Return the RHS, if it is greater than the LHS.

(?|:) :: (RealDimension n, LocallyScalable n a, LocallyScalable n b, SimpleSpace (Needle a), SimpleSpace (Needle b)) => RWDfblFuncValue n a b -> RWDfblFuncValue n a b -> RWDfblFuncValue n a b infixl 3

Try the LHS, if it is undefined use the RHS. This works analogously to the standard Alternative method

  (<|>) :: Maybe a -> Maybe a -> Maybe a
  Just x <|> _ = Just x
  _      <|> a = a
  

Basically a weaker and agent-ised version of backupRegions.

backupRegions :: (RealDimension n, LocallyScalable n a, LocallyScalable n b) => RWDiffable n a b -> RWDiffable n a b -> RWDiffable n a b

Replace the regions in which the first function is undefined with values from the second function.

Regions within a manifold

data Region s m

A pathwise connected subset of a manifold m, whose tangent space has scalar s.

smoothIndicator :: LocallyScalable ℝ q => Region ℝ q -> Differentiable ℝ q ℝ

Represent a Region by a smooth function which is positive within the region, and crosses zero at the boundary.

Evaluation of differentiable functions

discretisePathIn

Arguments

:: (WithField ℝ Manifold y, SimpleSpace (Needle y))

=> Int

Limit the number of steps taken in either direction. Note this will not cap the resolution but length of the discretised path.

-> ℝInterval

Parameter interval of interest.

-> (RieMetric ℝ, RieMetric y)

Inaccuracy allowance ε.

-> Differentiable ℝ ℝ y

Path specification.

-> [(ℝ, y)]

Trail of points along the path, such that a linear interpolation deviates nowhere by more as ε.

discretisePathSegs

Arguments

:: (WithField ℝ Manifold y, SimpleSpace (Needle y))

=> Int

Maximum number of path segments and/or points per segment.

-> (RieMetric ℝ, RieMetric y)

Inaccuracy allowance δ for arguments (mostly relevant for resolution of discontinuity boundaries – consider it a “safety margin from singularities”), and ε for results in the target space.

-> RWDiffable ℝ ℝ y

Path specification. It is recommended that this function be limited to a compact interval (e.g. with ?>, ?< and ?->). For many functions the discretisation will even work on an infinite interval: the point density is exponentially decreased towards the infinities. But this is still pretty bad for performance.

-> ([[(ℝ, y)]], [[(ℝ, y)]])

Discretised paths: continuous segments in either direction

continuityRanges

Arguments

:: WithField ℝ Manifold y

=> Int

Max number of exploration steps per region

-> RieMetric ℝ

Needed resolution of boundaries

-> RWDiffable ℝ ℝ y

Function to investigate

-> ([ℝInterval], [ℝInterval])

Subintervals on which the function is guaranteed continuous.

regionOfContinuityAround :: RWDiffable ℝ q x -> q -> Region ℝ q

analyseLocalBehaviour

Arguments

:: RWDiffable ℝ ℝ ℝ

-> ℝ

x₀ value.

-> Option ((ℝ, ℝ), ℝ -> Option ℝ)

f x₀, derivative (i.e. Taylor-1-coefficient), and reverse propagation of O (δ²) bound.

intervalImages

Arguments

:: Int

Max number of exploration steps per region

-> (RieMetric ℝ, RieMetric ℝ)

Needed resolution in (x,y) direction

-> RWDiffable ℝ ℝ ℝ

Function to investigate

-> ([(ℝInterval, ℝInterval)], [(ℝInterval, ℝInterval)])

(XInterval, YInterval) rectangles in which the function graph lies.