| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
Optics
Contents
Description
Synopsis
- module Optics.Optic
- module Optics.AffineFold
- module Optics.AffineTraversal
- module Optics.Fold
- module Optics.Getter
- module Optics.Iso
- module Optics.IxLens
- module Optics.IxGetter
- module Optics.IxAffineFold
- module Optics.IxAffineTraversal
- module Optics.IxFold
- module Optics.IxSetter
- module Optics.IxTraversal
- module Optics.Lens
- module Optics.ReversedLens
- module Optics.Prism
- module Optics.ReversedPrism
- module Optics.Review
- module Optics.Setter
- module Optics.Traversal
- module Optics.Operators
- module Optics.At
- module Optics.Cons
- module Optics.Each
- module Optics.Empty
- module Optics.Re
- module Optics.ReadOnly
- module Optics.Mapping
- module Optics.State
- module Optics.View
- module Optics.Zoom
- module Optics.Indexed
- module Optics.TH
- module Optics.Label
- module Data.Either.Optics
- module Data.Maybe.Optics
- module Data.Tuple.Optics
Introduction
Read on for a general introduction to the notion of optics, or if you are familiar with them already, you may wish to jump ahead to the "What is the abstract interface?" section below in Optics.
What are optics?
An optic is a first-class, composable notion of substructure. As a highly
abstract concept, the idea can be approached by considering several examples
of optics and understanding their common features. What are the possible
relationships between some "outer" type S and some "inner" type A?
(For simplicity we will initially ignore the possibility of type-changing
update operations, which change A to some other type B and hence change
S to some other type T. These are fully supported by the library, at the
cost of some extra type parameters.)
Optics.Iso: isomorphisms
First, S and A may be isomorphic, i.e. there exist mutually inverse
functions to convert S -> A and A -> S. This is a somewhat trivial
notion of substructure: A is just another way to represent "all of S".
An Iso' S AS and A, with the conversion
functions given by view and review. For example, given
newtype Age = Age Int
there is an isomorphism between the newtype and its representation:
coerced::Iso'AgeIntviewcoerced:: Age ->Intreviewcoerced::Int-> Age
Optics.Lens: generalised fields
If S is a simple product type (i.e. it has a single constructor with one or
more fields), A may be a single field of S. More generally, A may be
"part of S" in the sense that S is isomorphic to the pair (A,C) for
some type C representing the other fields. In this case, there is a
projection function S -> A for getting the value of the field, but the
update function (setting the value of the field) requires the "rest of S"
and so has type A -> S -> S.
A Lens' S AA being a field of S, with the
projection function given by view and the update function by set. For
example, for the pair type (X,Y) there are lenses for each component:
_1::Lens'(X,Y) X_2::Lens'(X,Y) Yview_1:: (X,Y) -> Xset_2:: Y -> (X,Y) -> (X,Y)
(Note that the update function could arguably have the more precise type A
-> C -> S, since we do not expect the result of setting a field to depend on
the previous value of the field. However, making C explicit turns out to
be awkward, so instead we impose laws to require that the result of setting
the field depends only on C, and, more generally, that the lens behaves as
we would expect.)
Optics.Prism: generalised constructors
If S is a simple sum type (i.e. it has one or more constructors, each with
a single field), A may be the type of the field for a single constructor of
S. More generally, S may be isomorphic to the disjoint union Either D
A for some type D representing the other constructors. In this case,
projecting out A from S (pattern-matching on the constructor) may fail,
so it has type S -> Maybe A. In the reverse direction we have a function
of type A -> S representing the constructor itself.
A Prism' S AA being a constructor of S,
with the partial projection function given by preview and the constructor
function given by review. For example, for the type Either X Y
_Left::Prism'(EitherX Y) X_Right::Prism'(EitherX Y) Ypreview_Left::EitherX Y ->MaybeXreview_Right:: Y ->EitherX Y
Optics.Traversal: multiple substructures
Alternatively, S may "contain" the substructure A a variable number of
times. In this case, the projection function extracts the (possibly zero or
many) elements so has type S -> [A], while the update function may take
different values for different elements so has type (A -> A) -> S -> S
(though in fact more general formulations are possible).
A Traversal' S AA being contained in S
perhaps multiple times, with the list of values given by toListOf and the
update function given by over . For example, for the type Maybe X there
is a traversal that may return zero or one element:
traversed::Traversal'(MaybeX) XtoListOftraversed::MaybeX -> [X]overtraversed:: (X -> X) ->MaybeX ->MaybeX
(In fact, traversals of at most one element are known as affine traversals, see Optics.AffineTraversal.)
In general
So far we have seen four different kinds of optic or "notions of substructure", and many more are possible. Observe the important properties they have in common:
- There are subtyping relationships between different optic kinds. Any
isomorphism is trivially a lens and a prism (with no other fields or
constructors, respectively). Any lens is a traversal (where the list of
elements is always a singleton list), and any prism is also a traversal
(where there will be zero or one element depending on whether the
constructor matches). This was implicit in the fact that we
used the same operators in multiple cases:
viewgives the projection function of both an isomorphism and a lens, but cannot be applied to a traversal. - Optics can be composed. If
Sis isomorphic toUandUis isomorphic toAthenSis isomorphic toA, and similarly for other optic kinds. - Composition and subtyping interact: a lens and a prism can be composed, by
first thinking of them as traverals using the subtyping relationship. That
is, if
Shas a fieldU, andUhas a constructorA, thenScontains zero or oneAs that we can pick out with a traversal (but in general there is neither a lens fromStoAnor a prism). - Each optic kind can be described by certain operations it enables. For example lenses support projection and update, while prisms support partial projection and construction.
- Optics are subject to laws, which are necessary for the operations to make sense.
The point of the optics library is to capture this common pattern.
What is the abstract interface?
A key principle behind this library is the belief that optics are useful as an abstract concept, and that the purpose of types is to capture abstract concepts and make them useful. The programmer using optics should be able to think in terms of the abstract interface, rather than the details of the implementation, and implementation choices should (as far as possible) not dictate the interface.
Each optic kind is identified by a "tag type" (such as A_Lens), which is an
empty data type. The type of the actual optics (such as Lens) is obtained
by applying the Optic newtype wrapper to the tag type.
typeLenss t a b =OpticA_LensNoIxs t a b typeLens's a =Optic'A_LensNoIxs a
NoIx as the second parameter to Optic indicates that the optic is not
indexed. See the "Indexed optics" section below in Optics for
further discussion of indexed optics.
The details of the internal implementation of Optic are hidden behind an
abstraction boundary, so that the library can be used without needing to
think about the particular implementation choices.
Specification of optics interfaces
Each different kind of optic is documented in a separate module describing its abstract interface, in a standard format with at least formation, introduction, elimination, and well-formedness sections. See "Optic kinds" below in Optics for a list of these modules.
The formation sections contain type definitions. For example Optics.Lens defines:
-- Type synonym for a type-modifying lens. type
Lenss t a b =OpticA_LensNoIxs t a bThe introduction sections describe the canonical way to construct each particular optic. Continuing with a
Lensexample:-- Build a lens from a getter and a setter.
lens:: (s -> a) -> (s -> b -> t) ::Lenss t a bCorrespondingly, the elimination sections show how you can destruct the optic into the pieces from which it was constructed.
-- A
Lensis aSetterand aGetter, therefore you can specialise types to obtainview::Lenss t a b -> s -> aset::Lenss t a b -> b -> s -> tThe computation rules tie introduction and elimination forms together. These rules are automatically fulfilled by the library (for well-formed optics).
view(lensf g) s ≡ f sset(lensf g) a s ≡ g s aThe well-formedness sections describe the laws that each optic should obey. As far as possible, all optics provided by the library are well-formed, but in some cases this depends on invariants that cannot be expressed in types. Ill-formed optics might behave differently from what the computation rules specify.
For example, a
Lensshould obey three laws, known as GetPut, PutGet and PutPut. See the Optics.Lens module for their definitions. The user of thelensintroduction form must ensure that these laws are satisfied.- Some optic kinds have additional introduction forms, additional elimination forms or combinators sections, which give alternative ways to create and use optics of that kind. In principle these are expressible in terms of the canonical introduction and elimination rules.
- The subtyping section gives the "tag type" (such as
A_Lens), which in particular is accompanied byIsinstances that define the subtyping relationship discussed in the following section.
Subtyping
There is a subtyping relationship between optics, implemented using
typeclasses. The Is typeclass captures the property that one optic kind
can be used as another, and the castOptic function can be used to
explicitly cast between optic kinds. Is forms a partial order, represented
in the graph below. For example, a lens can be used as a traversal, so there
are arrows from Lens to Traversal (via AffineTraversal) and there is an
instance of Is A_Lens A_Traversal
Introduction forms (constructors) return a concrete optic kind, while elimination forms (destructors) are generally polymorphic in the optic kind they accept. This means that it is not normally necessary to explicitly cast between optic kinds. For example, we have
view::IskA_Getter=>Optic'k is s a -> s -> a
so view can be used with isomorphisms or lenses, as these can be converted
to a Getter.
If an explicit cast is needed, you can use castOptic. This arises when you
use optics of different kinds in a context that requires them to have the
same type. For example [ gives a type error (since
folded, traversed]A_Traversal is not A_Fold) but [
works.folded, castOptic traversed]
The optic kind module (e.g. Optics.Lens) does not list all ways to
construct or use particular the optic kind. For example, since a Lens is
also a Traversal, a Fold etc, so you can use traverseOf, preview and
many other combinators with lenses.
Subtype hierarchy
This graph gives an overview of the optic kinds and their subtype relationships:

In addition to the optic kinds included in the diagram, there are also
indexed variants such as IxLens, IxGetter, IxAffineTraversal,
IxTraversal, IxAffineFold, IxFold and IxSetter. These are explained
in more detail in the "Indexed optics" section below in Optics.
Composition
Since optics are not functions, they cannot be composed with the (.)
operator. Instead there is a separate composition operator (%). The
composition operator returns the common supertype of its arguments, or
generates a type error if the composition does not make sense.
The optic kind resulting from a composition is the least upper bound (join)
of the optic kinds being composed, if it exists. The Join type family
computes the least upper bound given two optic kind tags. For example the
Join of a Lens and a Prism is an AffineTraversal.
>>>:kind! Join A_Lens A_PrismJoin A_Lens A_Prism :: OpticKind = An_AffineTraversal
The join does not exist for some pairs of optic kinds, which means that they
cannot be composed. For example there is no optic kind above both Setter
and Fold:
>>>:kind! Join A_Setter A_FoldJoin A_Setter A_Fold :: OpticKind = (TypeError ...)
>>>:t mapped % folded... ...A_Setter cannot be composed with A_Fold ...
The (.) operator from Control.Category cannot be used to
compose optics either, because it would not support type-changing optics or
composing optics of different kinds.
Comparison with lens
The lens package is the best known Haskell library for optics, and
established many of the foundations on which the optics package builds (not
least in quite a bit of code having been directly ported). It defines optics
based on the van Laarhoven representation, where each optic kind is
introduced as a transparent type synonym for a complex polymorphic type,
for example:
type Lens s t a b = forall f. Functor f => (a -> f b) -> s -> f t
In contrast, optics tries to preserve an abstraction boundary between the
interface of optics and their implementation. Optic kinds are expressed
directly in the types, as Optic is an opaque newtype:
typeLenss t a b =OpticA_LensNoIxs t a b
The choice of representation of Optic is then an implementation detail, not
essential for understanding the library. (In fact, optics uses the
profunctor representation rather than the van Laarhoven representation;
this affects the optic kinds and operations that can be conveniently
supported, but not the essence of the design.)
Our design choice to use opaque rather than transparent abstractions leads to various consequences, both positive and negative, which are explored in the following subsections.
Advantages of the opaque design
Since the interface is deliberately chosen rather than to some extent
determined by the implementation, we are free to choose a more restricted
interface where doing so leads to conceptual simplicity. For example, in
lens, the view function can be used with a Fold provided the result
type has a Monoid instance, and the multiple targets of the Fold will be
combined monoidally. This behaviour can be confusing, so in optics a
Fold cannot be silently used as a Getter, and we prefer to have view
work on Getters and define a separate foldOf operator for use on
Folds. (But the gview function is available for users who may prefer
otherwise.)
In general, opaque abstractions lead to better results from type inference (the optic kind is preserved in the inferred type):
>>>:t traversed % to nottraversed % to not :: Traversable t => Optic A_Fold '[] (t Bool) (t Bool) Bool Bool
Error messages are domain-specific:
>>>set (to fst)... ...A_Getter cannot be used as A_Setter ...
Composing incompatible optics yields a sensible error:
>>>sets map % to not... ...A_Setter cannot be composed with A_Getter ...
Since Optic is a rank-1 type, it is easy to store optics in a
datastructure:
>>>:t [folded, backwards_ folded][folded, backwards_ folded] :: Foldable f => [Fold (f a) a]
It is possible to define aliases for optics without the monomorphism restriction spoiling the fun:
>>>let { myoptic = _1; p = ('x','y') } in (view myoptic p, set myoptic 'c' p)('x',('c','y'))
Finally, having an abstract interface gives more freedom of choice in the internal implementation. If there is a compelling reason to switch to an alternative representation, one can in principle do so without changing the interface.
Disadvantages of the opaque design
Since Optic is a newtype, other libraries that wish to define optics must
depend upon its definition. In contrast, with a transparent representation,
and since the van Laarhoven representations of lenses and traversals depend
only on definitions from base, it is possible for libraries to define them
without any extra library dependencies (although this does not hold for more
advanced optic kinds such as prisms or indexed optics). To address this, the
present library is split into a package optics-core, which has a minimal
dependency footprint intended for use in libraries, and the
"batteries-included" optics package for use in applications.
It is something of an amazing fact that the composition operator for
transparent optics is just function composition. Moreover, since Haskell
uses (.) for function composition, lens is able to support a pseudo-OOP
syntax. In contrast, optics must use a different composition operator
(%). Optic does not quite form a Category, thanks to
type-changing optics.
Rather than emerging naturally from the definitions, opportunities for
polymorphism have to be identified in advance and explicitly introduced using
type classes. Similarly, the set of optic kinds and the subtyping
relationships between them must be fixed in advance, and cannot be added to
in downstream libraries. Thus in a sense the opaque approach is more
restrictive than the transparent one. There are cases in lens where the
types work out nicely and permit abstraction-breaking-but-convenient
shortcuts, such as applying a Traversal as a traverse-like function,
whereas optics requires a call to traverseOf.
More specific differences
The sections above set out the major conceptual differences from the lens
package, and their advantages and disadvantages. Some more specific design
differences, which may be useful for comparison or porting code between the
libraries. This list is no doubt incomplete.
- The composition operator is (
%) rather than (.) and is defined asinfixl 9instead ofinfixr 9. - Fewer operators are provided, and some of them are not exported from the main Optics module. Import Optics.State.Operators if you want them.
- The
viewfunction and corresponding (^.) operator work only forGetters and have a more restricted type. The equivalent forFolds isfoldOf, and you can usepreviewforAffineFolds. Alternatively you can usegviewwhich is more compatible withviewfromlens, but it uses a type class to choose betweenview,previewandfoldOf. - Indexed optics are rather different, as described in the "Indexed optics" section below in Optics. All ordinary optics are "index-preserving", so there is no separate notion of an index-preserving optic.
Eachprovides indexed traversals.firstOffromlensis replaced byheadOf.concatOffromlensis omitted in favour of the more generalfoldOf.set'is a strict version ofset, notsetfor type-preserving optics.- Numbered lenses for accessing fields of tuples positionally are provided
only up to
_9, rather than_19. - There are four variants of
backwardsfor (indexed)Traversals andFolds:backwards,backwards_,ibackwardsandibackwards_. - There is no
Traversal1andFold1. - There are affine variants of (indexed) traversals and folds
(
AffineTraversal,AffineFold,IxAffineTraversalandIxAffineFold). An affine optic targets at most one value. Composing aLenswith aPrismproduces anAffineTraversal, so for examplematching(_1%_Left) - Functions
ifilteredandindicesare defined as optic combinators due to restrictions of internal representation. - We can't use
traverseas an optic directly. Instead there is aTraversalcalledtraversed. SimilarlytraverseOfmust be used to apply aTraversal, rather than simply using it as a function. - The
recombinator produces a different optic kind depending on the kind of the inputIso, for exampleReviewreverses toGetterwhile a reversedIsois still anIso. Thus there is no separatefromcombinator for reversingIsos. singular(isingularfor indexed optics) doesn't produce a partial lens that might fail with a runtime error, but an affine traversal.<>cannot be used to combineFolds, sosummingshould be used instead.
Other resources
- Through a Glass, Abstractly: Lenses and the Power of Abstraction a talk on the principles behind this library with accompanying slides by Adam Gundry (but note that the design details of
opticshave changed substantially since this talk was given) - Profunctors and Data Accessors a talk on basics of profunctors and how they relate to data accessors such as lenses, prisms and traversals by Andrzej Rybczak
- Profunctor Optics: Modular Data Accessors a paper by Matthew Pickering, Jeremy Gibbons and Nicolas Wu
- Glassery and Indexed Profunctor optics, blog posts by Oleg Grenrus
- The lens package by Edward Kmett and contributors
Using the library
To get started, you can just add optics as a dependency to your .cabal
file, and then:
import Optics
If you are writing a library for which it is important to keep the dependency
footprint minimal, you may wish to depend upon optics-core instead (and
perhaps optics-extra or optics-th), and then:
import Optics.Core
module Optics.Optic
Optic kinds
module Optics.AffineFold
module Optics.AffineTraversal
module Optics.Fold
module Optics.Getter
module Optics.Iso
module Optics.IxLens
module Optics.IxGetter
module Optics.IxAffineFold
module Optics.IxAffineTraversal
module Optics.IxFold
module Optics.IxSetter
module Optics.IxTraversal
module Optics.Lens
module Optics.ReversedLens
module Optics.Prism
module Optics.ReversedPrism
module Optics.Review
module Optics.Setter
module Optics.Traversal
Optic operators
module Optics.Operators
Optics utilities
At
An AffineTraversal to traverse a key in a map or an element of a
sequence:
>>>preview (ix 1) ['a','b','c']Just 'b'
a Lens to get, set or delete a key in a map:
>>>set (at 0) (Just 'b') (Map.fromList [(0, 'a')])fromList [(0,'b')]
and a Lens to insert or remove an element of a set:
>>>IntSet.fromList [1,2,3,4] & contains 3 .~ FalsefromList [1,2,4]
module Optics.At
Cons
Prisms to match on the left or right side of a list, vector or other
sequential structure:
>>>preview _Cons "abc"Just ('a',"bc")
>>>preview _Snoc "abc"Just ("ab",'c')
module Optics.Cons
Each
An IxTraversal for each element of a (potentially monomorphic) container.
>>>over each (*10) (1,2,3)(10,20,30)
module Optics.Each
Empty
A Prism for a container type that may be empty.
>>>isn't _Empty [1,2,3]True
module Optics.Empty
Re
Some optics can be reversed with re. This is mainly useful to invert
Isos:
>>>let _Identity = iso runIdentity Identity>>>view (_1 % re _Identity) ('x', "yz")Identity 'x'
Yet we can use a Lens as a Review too:
>>>review (re _1) ('x', "yz")'x'
In the following diagram, red arrows illustrate how re transforms optics.
The ReversedLens and ReversedPrism optic kinds are backwards versions
of Lens and Prism respectively, and are present so that re . re
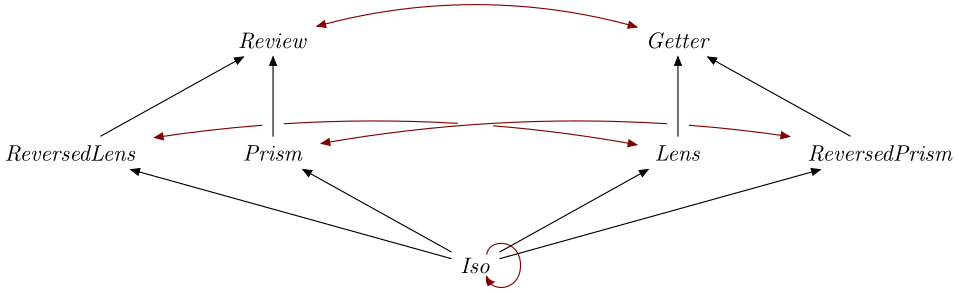
module Optics.Re
ReadOnly
Defines getting, which turns a read-write optic into its read-only
counterpart.
module Optics.ReadOnly
Mapping
module Optics.Mapping
Setter utilities for working in MonadState.
module Optics.State
View
A generalized view function gview, which returns a single result (like
view) if the optic is a Getter, a Maybe result (like preview) if
the optic is an AffineFold, or a monoidal summary of results (like
foldOf) if the optic is a Fold. In addition, it works for any
MonadReader, not just (->).
>>>gview _1 ('x','y')'x'
>>>gview _Left (Left 'x')Just 'x'
>>>gview folded ["a", "b"]"ab"
>>>runReaderT (gview _1) ('x','y') :: IO Char'x'
This module is experimental. Using the more type-restricted variants is encouraged where possible.
module Optics.View
Zoom
A class to zoom in, changing the State supplied
by many different monad transformers, potentially quite deep in a monad
transformer stack.
>>>flip execState ('a','b') $ zoom _1 $ equality .= 'c'('c','b')
module Optics.Zoom
Indexed optics
The optics library also provides indexed optics, which provide
an additional index value in mappings:
over::Setters t a b -> (a -> b) -> s -> tiover::IxSetteri s t a b -> (i -> a -> b) -> s -> t
Note that there aren't any laws about indices. Especially in compositions the same index may occur multiple times.
The machinery builds on indexed variants of Functor, Foldable, and Traversable classes:
FunctorWithIndex, FoldableWithIndex and TraversableWithIndex respectively.
There are instances for types in the boot libraries.
class (FoldableWithIndexi t,Traversablet) =>TraversableWithIndexi t | t -> i whereitraverse::Applicativef => (i -> a -> f b) -> t a -> f (t b)
Indexed optics can be used as regular ones, i.e. indexed optics gracefully downgrade to regular ones.
>>>toListOf ifolded "foo""foo"
>>>itoListOf ifolded "foo"[(0,'f'),(1,'o'),(2,'o')]
But there is also a combinator noIx to explicitly erase indices:
>>>:t (ifolded % simple)(ifolded % simple) :: FoldableWithIndex i f => Optic A_Fold '[i] (f b) (f b) b b
>>>:t noIx (ifolded % simple)noIx (ifolded % simple) :: FoldableWithIndex i f => Optic A_Fold NoIx (f b) (f b) b b
λ> :t noIx (ifolded % ifolded)
noIx (ifolded % ifolded)
:: (FoldableWithIndex i1 f1, FoldableWithIndex i2 f2) =>
Optic A_Fold NoIx (f1 (f2 b)) (f1 (f2 b)) b b
As the example above illustrates, regular and indexed optics have the same
tag in the first parameter of Optic, in this case A_Fold. Regular optics
simply don't have any indices. The provided type aliases IxLens,
IxGetter, IxAffineTraversal, IxAffineFold, IxTraversal, IxFold and
IxSetter are variants with a single index. In general, the second parameter
of the Optic newtype is a type-level list of indices, which will typically
be NoIx (the empty index list) or ( (a singleton list).WithIx i)
When two optics are composed with (%), the index lists are concatenated.
Thus composing an unindexed optic with an indexed optic preserves the
indices, or composing two indexed optics retains both indices:
λ> :t (ifolded % ifolded)
(ifolded % ifolded)
:: (FoldableWithIndex i1 f1, FoldableWithIndex i2 f2) =>
Optic A_Fold '[i1, i2] (f1 (f2 b)) (f1 (f2 b)) b b
In order to use such an optic, it is necessary to flatten the indices into a
single index using icompose or a similar function:
λ> :t icompose (,) (ifolded % ifolded)
icompose (,) (ifolded % ifolded)
:: (FoldableWithIndex i1 f1, FoldableWithIndex i2 f2) =>
Optic A_Fold (WithIx (i1, i2)) (f1 (f2 b)) (f1 (f2 b)) b b
For example:
>>>itoListOf (icompose (,) (ifolded % ifolded)) [['a','b'], ['c', 'd']][((0,0),'a'),((0,1),'b'),((1,0),'c'),((1,1),'d')]
Alternatively, you can use one of the (<%) or (%>) operators to compose
indexed optics and pick the index to retain, or the (<%>) operator to
retain a pair of indices:
>>>itoListOf (ifolded <% ifolded) [['a','b'], ['c', 'd']][(0,'a'),(0,'b'),(1,'c'),(1,'d')]
>>>itoListOf (ifolded %> ifolded) [['a','b'], ['c', 'd']][(0,'a'),(1,'b'),(0,'c'),(1,'d')]
>>>itoListOf (ifolded <%> ifolded) [['a','b'], ['c', 'd']][((0,0),'a'),((0,1),'b'),((1,0),'c'),((1,1),'d')]
In the diagram below, the optics hierarchy is amended with these (singly) indexed variants (in blue).
Orange arrows mean
"can be used as one, assuming it's composed with any optic below the
orange arrow first". For example. _1 is not an indexed fold, but
itraversed % _1
>>>let fst' = _1 :: Lens (a, c) (b, c) a b>>>:t fst' % itraversedfst' % itraversed :: TraversableWithIndex i f => Optic A_Traversal '[i] (f a, c) (f b, c) a b
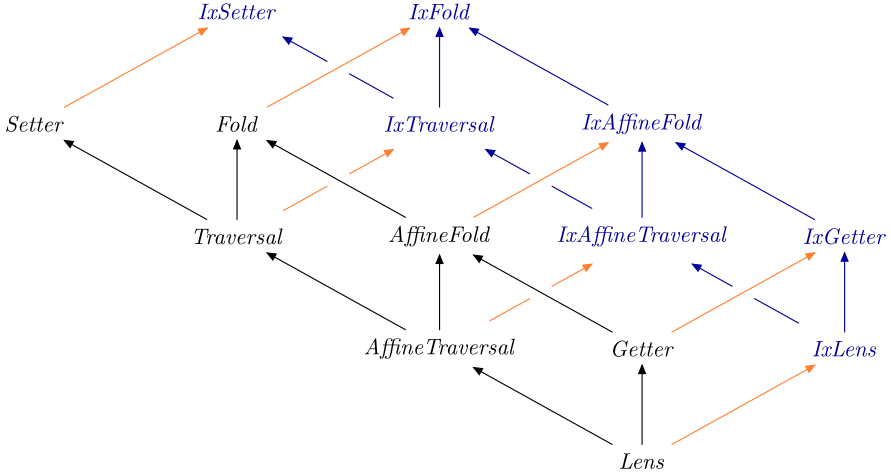
module Optics.Indexed
Generation of optics
...with Template Haskell
module Optics.TH
...with OverloadedLabels
module Optics.Label
Optics for concrete base types
module Data.Either.Optics
module Data.Maybe.Optics
module Data.Tuple.Optics
Cheat sheet
The following table summarizes the key optic kinds and their combinators. It is based on a similar table for the lens package.
A Lens can be used as a Getter, Setter, Fold and Traversal.
| Combinator | Indexed | Notes |
|---|---|---|
| Getters | ||
to
| ito
| Build a Getter / IxGetter from a plain
function. |
view / ^. | iview | View a single target. |
views | iviews | View after applying a function. |
| Setters | ||
sets
| isets
| Build a Setter / IxSetter from an update
function. |
mapped
| imapped
| Build a Setter from the Functor class, or an
IxSetter from FunctorWithIndex. |
set / .~ | iset | Replace target(s) with value. |
over / %~ | iover | Modify target(s) by applying a function. |
| Folds | ||
folded
| ifolded
| Build a Fold from the Foldable class, or an
IxFold from FoldableWithIndex. |
toListOf / ^.. | itoListOf | Return a list of the target(s). |
| AffineFolds | ||
afolding
| iafolding
| Build an AffineFold / IxAffineFold from a
partial function. |
preview / ^? | ipreview | Match the target or return Nothing. |
previews | ipreviews | Preview after applying a function. |
| Traversals | ||
traversed
| itraversed
| Build a Traversal from the Traversable class,
or an IxTraversal from TraversableWithIndex. |
traverseOf | itraverseOf | Update target(s) with an Applicative. |
| Prisms | ||
prism | Build a Prism from a constructor and matcher. | |
review / # | Use a Prism to construct the sum type. | |
For setting/modifying using a Setter, a variety of combinators are available
in Optics.State and Optics.State.Operators. The latter are not exported
by the main Optics module, so must be imported explicitly.
| Lazy | Strict | Stateful | Stateful returning new value | Stateful returning old value | Notes |
|---|---|---|---|---|---|
set / .~ | set' / !~ | assign / .= | <.= | <<.= | Replace target(s) with value. |
over / %~ | over' / %!~ | modifying / %= | <%= | <<%= | Modify target(s) by applying a function. |
?~ | ?!~ | ?= | <?= | <<?= | Replace target(s) with Just a value. |