| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
Optics.ReversedLens
Description
Synopsis
- type ReversedLens s t a b = Optic A_ReversedLens NoIx s t a b
- type ReversedLens' t b = Optic' A_ReversedLens NoIx t b
- data A_ReversedLens
Formation
type ReversedLens s t a b = Optic A_ReversedLens NoIx s t a b Source #
Type synonym for a type-modifying reversed lens.
type ReversedLens' t b = Optic' A_ReversedLens NoIx t b Source #
Type synonym for a type-preserving reversed lens.
Introduction
There is no canonical introduction form for ReversedLens, but you can use
re to construct one from a Lens:
(\ f g ->re(lensf g)) :: (b -> t) -> (b -> s -> a) ->ReversedLenss t a b
Elimination
A ReversedLens is a Review, so you can specialise types to obtain:
review::ReversedLens's a -> a -> s
There is no corresponding optic kind for a backwards
Setter, but a reversed set is definable
using re:
set.re::ReversedLenss t a b -> s -> b -> a
Computation
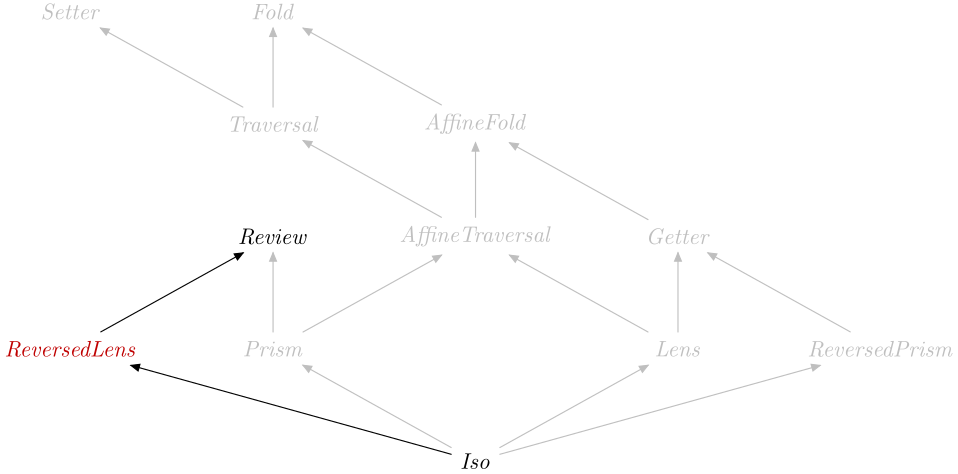
Subtyping
data A_ReversedLens Source #
Tag for a reversed lens.
Instances
| ReversibleOptic A_ReversedLens Source # | |
Defined in Optics.Re Associated Types type ReversedOptic A_ReversedLens = (r :: Type) Source # Methods re :: AcceptsEmptyIndices "re" is => Optic A_ReversedLens is s t a b -> Optic (ReversedOptic A_ReversedLens) is b a t s Source # | |
| Is A_ReversedLens A_Review Source # | |
Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy A_ReversedLens A_Review p -> (Constraints A_ReversedLens p -> r) -> Constraints A_Review p -> r Source # | |
| Is An_Iso A_ReversedLens Source # | |
Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy An_Iso A_ReversedLens p -> (Constraints An_Iso p -> r) -> Constraints A_ReversedLens p -> r Source # | |
| type ReversedOptic A_ReversedLens Source # | |
Defined in Optics.Re | |