| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
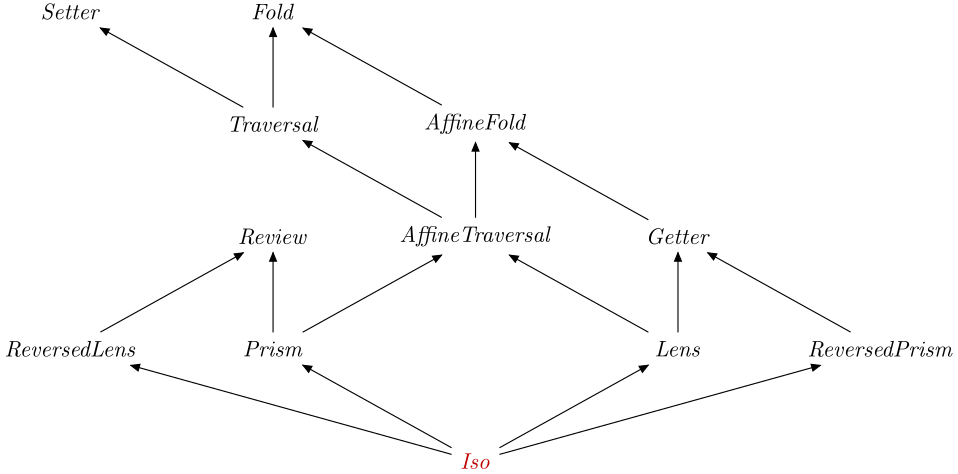
Optics.Iso
Contents
Description
An Isomorphism expresses the fact that two types have the
same structure, and hence can be converted from one to the other in
either direction.
Synopsis
- type Iso s t a b = Optic An_Iso NoIx s t a b
- type Iso' s a = Optic' An_Iso NoIx s a
- iso :: (s -> a) -> (b -> t) -> Iso s t a b
- equality :: (s ~ a, t ~ b) => Iso s t a b
- simple :: Iso' a a
- coerced :: (Coercible s a, Coercible t b) => Iso s t a b
- coercedTo :: forall a s. Coercible s a => Iso' s a
- coerced1 :: forall f s a. (Coercible s (f s), Coercible a (f a)) => Iso (f s) (f a) s a
- non :: Eq a => a -> Iso' (Maybe a) a
- non' :: Prism' a () -> Iso' (Maybe a) a
- anon :: a -> (a -> Bool) -> Iso' (Maybe a) a
- curried :: Iso ((a, b) -> c) ((d, e) -> f) (a -> b -> c) (d -> e -> f)
- uncurried :: Iso (a -> b -> c) (d -> e -> f) ((a, b) -> c) ((d, e) -> f)
- flipped :: Iso (a -> b -> c) (a' -> b' -> c') (b -> a -> c) (b' -> a' -> c')
- involuted :: (a -> a) -> Iso' a a
- class Bifunctor p => Swapped p where
- withIso :: Iso s t a b -> ((s -> a) -> (b -> t) -> r) -> r
- au :: Functor f => Iso s t a b -> ((b -> t) -> f s) -> f a
- under :: Iso s t a b -> (t -> s) -> b -> a
- mapping :: (Functor f, Functor g) => Iso s t a b -> Iso (f s) (g t) (f a) (g b)
- data An_Iso :: OpticKind
Formation
Introduction
iso :: (s -> a) -> (b -> t) -> Iso s t a b Source #
Build an iso from a pair of inverse functions.
If you want to build an Iso from the van Laarhoven representation, use
isoVL from the optics-vl package.
Elimination
An Iso is in particular a Getter, a
Review and a Setter, therefore you can
specialise types to obtain:
view::Iso's a -> s -> areview::Iso's a -> a -> s
over::Isos t a b -> (a -> b) -> s -> tset::Isos t a b -> b -> s -> t
If you want to view a type-modifying Iso that is
insufficiently polymorphic to be used as a type-preserving Iso', use
getting:
view.getting::Isos t a b -> s -> a
Computation
Well-formedness
The functions translating back and forth must be mutually inverse:
viewi .reviewi ≡idreviewi .viewi ≡id
Additional introduction forms
equality :: (s ~ a, t ~ b) => Iso s t a b Source #
Capture type constraints as an isomorphism.
Note: This is the identity optic:
>>>:t view equalityview equality :: a -> a
coerced :: (Coercible s a, Coercible t b) => Iso s t a b Source #
Data types that are representationally equal are isomorphic.
>>>view coerced 'x' :: Identity CharIdentity 'x'
coercedTo :: forall a s. Coercible s a => Iso' s a Source #
Type-preserving version of coerced with type parameters rearranged for
TypeApplications.
>>>newtype MkInt = MkInt Int deriving Show
>>>over (coercedTo @Int) (*3) (MkInt 2)MkInt 6
coerced1 :: forall f s a. (Coercible s (f s), Coercible a (f a)) => Iso (f s) (f a) s a Source #
Special case of coerced for trivial newtype wrappers.
>>>over (coerced1 @Identity) (++ "bar") (Identity "foo")Identity "foobar"
non :: Eq a => a -> Iso' (Maybe a) a Source #
If v is an element of a type a, and a' is a sans the element v,
then non vMaybe a'a.
non≡non'.only
Keep in mind this is only a real isomorphism if you treat the domain as being
Maybe (a sans v)
This is practically quite useful when you want to have a Map where
all the entries should have non-zero values.
>>>Map.fromList [("hello",1)] & at "hello" % non 0 %~ (+2)fromList [("hello",3)]
>>>Map.fromList [("hello",1)] & at "hello" % non 0 %~ (subtract 1)fromList []
>>>Map.fromList [("hello",1)] ^. at "hello" % non 01
>>>Map.fromList [] ^. at "hello" % non 00
This combinator is also particularly useful when working with nested maps.
e.g. When you want to create the nested Map when it is missing:
>>>Map.empty & at "hello" % non Map.empty % at "world" ?~ "!!!"fromList [("hello",fromList [("world","!!!")])]
and when have deleting the last entry from the nested Map mean
that we should delete its entry from the surrounding one:
>>>Map.fromList [("hello", Map.fromList [("world","!!!")])] & at "hello" % non Map.empty % at "world" .~ NothingfromList []
It can also be used in reverse to exclude a given value:
>>>non 0 # rem 10 4Just 2
>>>non 0 # rem 10 5Nothing
Since: 0.2
non' :: Prism' a () -> Iso' (Maybe a) a Source #
non' pnon (p # ())Prism
This function generates an isomorphism between Maybe (a | isn't p a)a.
>>>Map.singleton "hello" Map.empty & at "hello" % non' _Empty % at "world" ?~ "!!!"fromList [("hello",fromList [("world","!!!")])]
>>>Map.fromList [("hello", Map.fromList [("world","!!!")])] & at "hello" % non' _Empty % at "world" .~ NothingfromList []
Since: 0.2
anon :: a -> (a -> Bool) -> Iso' (Maybe a) a Source #
anon a pnon a
anona ≡non'.nearlya
This function assumes that p a holds TrueMaybe (a | not (p a))a.
>>>Map.empty & at "hello" % anon Map.empty Map.null % at "world" ?~ "!!!"fromList [("hello",fromList [("world","!!!")])]
>>>Map.fromList [("hello", Map.fromList [("world","!!!")])] & at "hello" % anon Map.empty Map.null % at "world" .~ NothingfromList []
Since: 0.2
flipped :: Iso (a -> b -> c) (a' -> b' -> c') (b -> a -> c) (b' -> a' -> c') Source #
The isomorphism for flipping a function.
>>>(view flipped (,)) 1 2(2,1)
Additional elimination forms
withIso :: Iso s t a b -> ((s -> a) -> (b -> t) -> r) -> r Source #
Extract the two components of an isomorphism.
Combinators
Subtyping
data An_Iso :: OpticKind Source #
Tag for an iso.
Instances