| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
Optics.AffineFold
Contents
Description
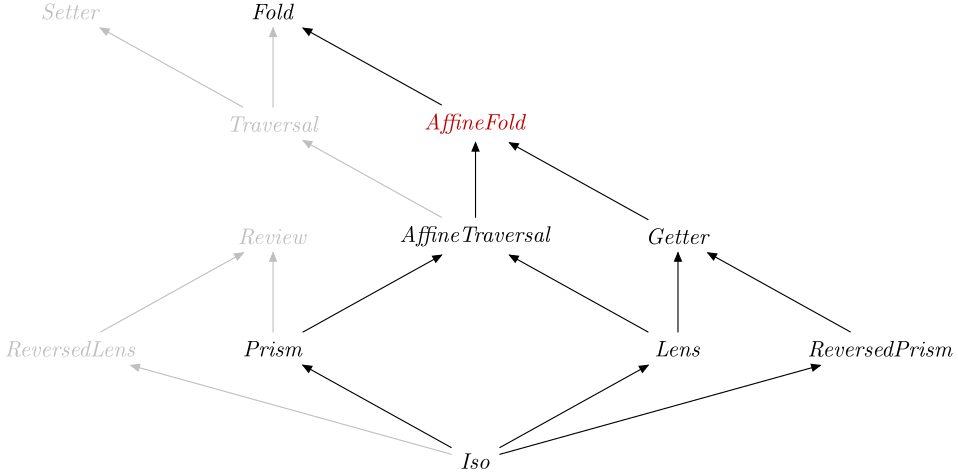
An AffineFold is a Fold that contains at most one
element, or a Getter where the function may be
partial.
Synopsis
- type AffineFold s a = Optic' An_AffineFold NoIx s a
- afolding :: (s -> Maybe a) -> AffineFold s a
- preview :: Is k An_AffineFold => Optic' k is s a -> s -> Maybe a
- previews :: Is k An_AffineFold => Optic' k is s a -> (a -> r) -> s -> Maybe r
- afoldVL :: (forall f. Functor f => (forall r. r -> f r) -> (a -> f u) -> s -> f v) -> AffineFold s a
- filtered :: (a -> Bool) -> AffineFold a a
- atraverseOf_ :: (Is k An_AffineFold, Functor f) => Optic' k is s a -> (forall r. r -> f r) -> (a -> f u) -> s -> f ()
- isn't :: Is k An_AffineFold => Optic' k is s a -> s -> Bool
- afailing :: (Is k An_AffineFold, Is l An_AffineFold) => Optic' k is s a -> Optic' l js s a -> AffineFold s a
- data An_AffineFold :: OpticKind
Formation
type AffineFold s a = Optic' An_AffineFold NoIx s a Source #
Type synonym for an affine fold.
Introduction
afolding :: (s -> Maybe a) -> AffineFold s a Source #
Create an AffineFold from a partial function.
>>>preview (afolding listToMaybe) "foo"Just 'f'
Elimination
preview :: Is k An_AffineFold => Optic' k is s a -> s -> Maybe a Source #
Retrieve the value targeted by an AffineFold.
>>>let _Right = prism Right $ either (Left . Left) Right
>>>preview _Right (Right 'x')Just 'x'
>>>preview _Right (Left 'y')Nothing
previews :: Is k An_AffineFold => Optic' k is s a -> (a -> r) -> s -> Maybe r Source #
Retrieve a function of the value targeted by an AffineFold.
Computation
Additional introduction forms
afoldVL :: (forall f. Functor f => (forall r. r -> f r) -> (a -> f u) -> s -> f v) -> AffineFold s a Source #
Obtain an AffineFold by lifting traverse_ like function.
afoldVL.atraverseOf_≡idatraverseOf_.afoldVL≡id
Since: 0.3
filtered :: (a -> Bool) -> AffineFold a a Source #
Filter result(s) of a fold that don't satisfy a predicate.
Additional elimination forms
atraverseOf_ :: (Is k An_AffineFold, Functor f) => Optic' k is s a -> (forall r. r -> f r) -> (a -> f u) -> s -> f () Source #
Traverse over the target of an AffineFold, computing a Functor-based
answer, but unlike atraverseOf do not construct a
new structure.
Since: 0.3
isn't :: Is k An_AffineFold => Optic' k is s a -> s -> Bool Source #
Check to see if this AffineFold doesn't match.
>>>isn't _Just NothingTrue
Monoid structure
AffineFold admits a monoid structure where afailing combines folds
(returning a result from the second fold only if the first returns none)
and the identity element is ignored (which
returns no results).
Note: There is no summing equivalent that returns an
AffineFold, because it would not need to return more than one result.
There is no Semigroup or Monoid instance for AffineFold, because
there is not a unique choice of monoid to use that works for all optics,
and the (<>) operator could not be used to combine optics of different
kinds.
afailing :: (Is k An_AffineFold, Is l An_AffineFold) => Optic' k is s a -> Optic' l js s a -> AffineFold s a infixl 3 Source #
Try the first AffineFold. If it returns no entry, try the second one.
>>>preview (ix 1 % re _Left `afailing` ix 2 % re _Right) [0,1,2,3]Just (Left 1)
>>>preview (ix 42 % re _Left `afailing` ix 2 % re _Right) [0,1,2,3]Just (Right 2)
Subtyping
data An_AffineFold :: OpticKind Source #
Tag for an affine fold.
Instances